Matrices
1. Notion de matrice
1.1. Sur un exemple
- Pour faire 20 crèpes :
- 3 œufs,
- 30 cl de lait,
- 300 grammes de farine.
- Pour faire 1 gâteau :
- 5 œufs,
- 20 cl de lait,
- 400 grammes de farine.
Ces données peuvent être représentées sous la forme d’un tableau :
| Ingrédients pour | 20 crêpes | 1 gâteau |
|---|---|---|
| œufs | 3 | 5 |
| lait (en cl) | 30 | 20 |
| farine | 300 | 400 |
Mathématiquement, on peut voir ces valeurs sous la forme d’une matrice. Il suffit d’enlever les titres.
$$ R = \begin{pmatrix} 3 & 5 \\\\ 30 & 20 \\\\ 300 & 400 \end{pmatrix} $$
$R$ est une matrice « 3×2 » (se lit « trois deux » ou « trois par deux », mais pas « 6 »). C’est le type ou la taille de la matrice.
1.2. Définition
Une matrice à $n$ lignes et $p$ colonnes est un tableau de nombres (réels, complexes, booléens…). On dit qu’elle est de type ou de taille $n×p$.
Le terme général d’une matrice $A$ est souvent noté $\left(a_{ij}\right)_{ \begin{array}{c} 1 \le i \le n \\\\ 1 \le j \le p \end{array}}$ et dans ce cas, on a :
$$ A = \begin{pmatrix} a_{11} & a_{12} & \cdots & \cdots & a_{1j} & \cdots & a_{1p} \\\\ a_{21} & a_{22} & \cdots & \cdots & a_{2j} & \cdots & a_{2p} \\\\ \vdots & \vdots & & & \vdots & & \vdots \\\\ a_{i1} & a_{i2} & \cdots & \cdots & a_{ij} & \cdots & a_{ip} \\\\ \vdots & \vdots & & & \vdots & & \vdots \\\\ a_{n1} & a_{n2} & \cdots & \cdots & a_{nj} & \cdots & a_{np} \end{pmatrix}$$
Remarques :
- Attention, la numérotation des termes, ou coefficients de la matrice commence à 1.
- Observer le contenu de la ligne $i$ et celui de la colonne $j$.
- Le type de la matrice ne concerne pas la nature des nombres qu’elle contient (réels, complexes, booléens…).
- Cas particuliers :
- si $n=p$, la matrice est dite carrée,
- si $n=1$, elle est dite matrice ligne, ou vecteur ligne,
- si $p=1$, elle est dite matrice colonne, ou vecteur colonne.
1.3. Égalité matricielle
Soit deux matrices $A$ et $B$. $A=B$ signifie :
- $A$ et $B$ sont de même taille,
- pour tous $i$ et $j$ tels que $1 \le i \le n$ et $1 \le j \le p$, $a_{ij} = b_{ij}$.
2. Calcul matriciel
2.1. Somme de matrices
2.1.1. Sur l’exemple
Supposons que l’on veuille augmenter les quantités de nos recettes :
$$ R' = \begin{pmatrix} 3+1 & 5+1 \\\\ 30+5 & 20+15 \\\\ 300+100 & 400-100 \end{pmatrix} $$
On pourrait écrire $ R' = R + A $, avec
$$ A = \begin{pmatrix} 1 & 1 \\\\ 5 & 15 \\\\ 100 & -100 \end{pmatrix} $$
2.1.2. Définition
Si $A$ et $B$ sont deux matrices $n×p$, la matrice somme de $A$ et $B$ est notée $A+B$ et a pour terme général :
$$\left(a_{ij} + b_{ij}\right)_{ \begin{array}{c} 1 \le i \le n \\\\ 1 \le j \le p \end{array}}$$
2.1.3. Propriétés
- L’addition des matrices est :
- commutative : pour toutes matrices $A$ et $B$ de même taille, on a $A+B = B+A$,
- associative : pour toutes matrices $A$, $B$ et $C$ de même taille, on a $(A+B)+C = A+(B+C)$, que l’on notera $A+B+C$.
- L’addition a un élément neutre, la matrice nulle.
- On note $0_{n×p}$ la matrice $n×p$ dont tous les coefficients sont nuls.
- S’il n’y a pas ambiguïté, on la note simplement $0$.
2.2. Produit d’une matrice par un nombre
2.2.1. Sur l’exemple
On peut vouloir doubler la quantité de chaque ingrédient. Voire ajouter cinquante pourcents (en multipliant par 1,5), ou diviser les quantités par 10 (en multipliant par 0,1 ou $\frac{1}{10}$). Il suffit pour cela de multiplier tous les coefficients par le même nombre (2 pour doubler; 1,5 pour ajouter 50% ou 0,1 pour diviser par 10).
$ R' = \begin{pmatrix} 2×3 & 2×5 \\\\ 2×30 & 2×20 \\\\ 2×300 & 2×400 \end{pmatrix} $ $ R'' = \begin{pmatrix} 1,5×3 & 1,5×5 \\\\ 1,5×30 & 1,5×20 \\\\ 1,5×300 & 1,5×400 \end{pmatrix} $ $ R''' = \begin{pmatrix}\frac{1}{10}×3 &\frac{1}{10}×5 \\\\\frac{1}{10}×30 &\frac{1}{10}×20 \\\\\frac{1}{10}×300 &\frac{1}{10}×400 \end{pmatrix} $
On écrira $2×R$, $1,5×R$ ou $\frac{1}{10} R$.
2.2.2. Définition
Si $A$ est une matrice $n×p$ et $t$ un nombre, la matrice produit de $A$ par $t$ est notée $t×A$ ou $tA$ et a pour terme général :
$$\left(t × a_{ij}\right)_{ \begin{array}{c} 1 \le i \le n \\\\ 1 \le j \le p \end{array}}$$
C’est un produit dit externe.
2.2.3. Propriétés
Si deux matrices $A$ et $B$ sont de taille $n×p$, et $t_1$ et $t_2$ sont deux nombres, alors on a :
- $(t_1 + t_2)A = t_1 A + t_2 A$,
- $t_1 (A + B) = t_1 A + t_1 B$,
- $t_1(t_2 A) = (t_1×t_2) A$, noté simplement $t_1 t_2 A$.
2.2.4. Remarques
- Si $t=0$, alors pour toute matrice $A$ de type $n×p$, on a : $$t×A = 0×A = 0_{n×p}$$
- Si $t=1$, alors $t×A = 1×A = A$.
- Si $t=2$, alors $2A = A+A$, si $t=3$, $3A = A+A+A$…
- Si $t \in \mathbb N$, $tA = \underbrace{A+A+…+A}_{\text{t fois}}$.
- Si $t=-1$, alors $tA = (-1)×A$, que l’on note simplement $-A$.
C'est la matrice opposée de $A$.
En effet, en calculant le terme général de $A + (-1)×A$, on trouve bien la matrice nulle, ce qui fait bien de $(-1)×A$ l’opposée de $A$. - On définit au passage la différence de deux matrices (ajout de l’opposé) : $$A-B = A + (-1)×B$$ Ce qui se traduit simplement par la matrice de terme général : $$\left(a_{ij} - b_{ij}\right)_{ \begin{array}{c} 1 \le i \le n \\\\ 1 \le j \le p \end{array}}$$
2.3. Produit de deux matrices
2.3.1. Sur l’exemple
On doit faire les courses à la fois pour la maison et pour le goûter organisé la semaine prochaine.
| Pour la maison | Pour le lycée |
|---|---|
| 40 crêpes (2×) | 60 crêpes (3×) |
| 1 gâteau | 4 gâteaux |
Calculons :
| maison | lycée | |||||||||
| crêpes | gâteaux | total | crêpes | gâteaux | total | |||||
| œufs | 3 | ×2 | 5 | ×1 | 11 | 3 | ×3 | 5 | ×4 | 29 |
| lait | 30 | ×2 | 20 | ×1 | 80 | 30 | ×3 | 20 | ×4 | 170 |
| farine | 300 | ×2 | 400 | ×1 | 1000 | 300 | ×3 | 400 | ×4 | 2500 |
On peut présenter le calcul ainsi : la première matrice en bas à gauche, et la deuxième en haut à droite.
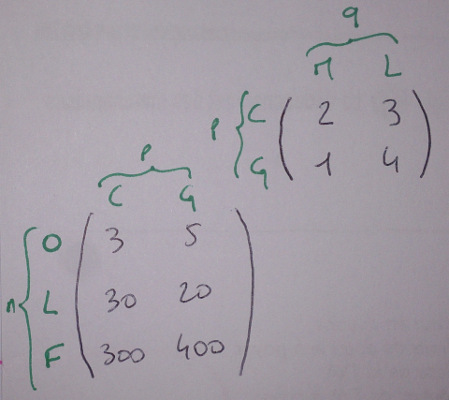
Et l’effectuer ainsi :
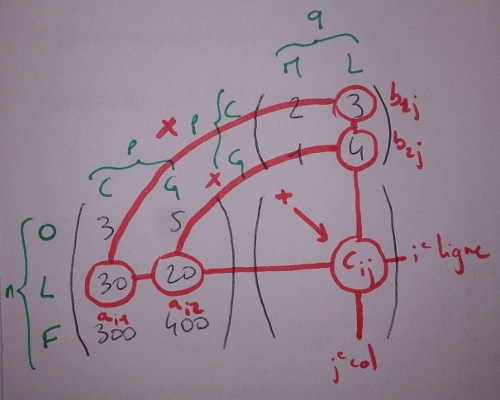
On retrouve bien la quantité de lait pour le lycée : 30×3 + 20×4 = 130.
Vérifier qu’avec cette mise en place, on obtient bien les autres quantités.
2.3.2. Définition
Soit $A$ une matrice $n×p$ et $B$ une matrice $p×q$.
Le produit matriciel de $A$ par $B$ est noté $A×B$, ou plus simplement $AB$, et est la matrice $n×q$ de terme général $\left(c_{ij}\right)_{ \begin{array}{c} 1 \le i \le n \\\\ 1 \le j \le q \end{array}}$ avec :
$$\begin{aligned} c_{ij} &= a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{ip} b_{pj} \\\\ &= \sum\limits_{k=1}^p a_{ik} b_{kj} \end{aligned}$$
2.3.3. Remarques
- La mise en place du produit matriciel est réservée au produit matriciel.
- La matrice de gauche reste à gauche (ou en bas à gauche), la matrice de droite reste à droite (en haut à droite).
- Le nombre de colonnes de la première matrice doit être égal au nombre de lignes de la deuxième.
- Au niveau des tailles, on a : $(n×p)×(p×q)=(n×q)$.
- Au niveau de la complexité du calcul :
- un seul terme de la matrice produit nécessite p multiplications et p-1 additions,
- le calcul de la matrice produit nécessite donc n×q×p multiplications et n×q×(p-1) additions.
2.3.4. Interprétation
Dans certains exercices, on demande d’interpréter les valeurs obtenues après un produit de deux matrices.
- S'il y a plusieurs valeurs à décrire, expliquer à quoi elles correspondent.
- Expliquer dans quel but, à quelle occasion...
- Pour l’idée « d’écrasement » ou de « qui n'apparait plus » après le produit, dire « tous trucs confondus » (« lycée ou maison confondus » pour l’exemple des recettes et les courses).
2.3.5. Propriétés
Avec un nombre t et trois matrices A, B et C, de tailles compatibles pour les produits :
- (AB)C = A(BC), que l’on notera simplement ABC
- A(B+C) = AB + AC
- (A+B)C = AC + BC
- (tA)B = t(AB) = A(tB), que l’on notera simplement tAB
- Attention, ce produit n’est pas commutatif !
Il y a deux raisons à cela :- la taille des matrices, car dans le cas où n≠q le calcul n’a pas de sens,
- même si les matrices sont carrées, elles peuvent ne pas commuter. Ici,
AB≠BA :
$$ A = \begin{pmatrix} 1 & 0 \\\\ 0 & 0 \end{pmatrix} ; B = \begin{pmatrix} 1 & 0 \\\\ 1 & 0 \end{pmatrix} $$
- Dans $\mathbb R$, $xy=0$ si et seulement si $x=0$ ou $y=0$ (« un produit
est nul si et seulement si au moins un des termes est nul »).
Mais chez les matrices, ce n’est plus vrai. Ici, A≠0 et B≠0, mais pourtant AB=0 :
$$ A = \begin{pmatrix} 1 & 0 \\\\ 0 & 0 \end{pmatrix} ; B = \begin{pmatrix} 0 & 0 \\\\ 0 & 1 \end{pmatrix} $$
2.3.6. Matrice(s) unité
2.3.6.1. Recherche
Si $0_{n×p}$ est l’élément neutre pour l’addition. Cherchons l’élément neutre pour la multiplication. On le notera $I_{n×p}$, ou, s’il n’y a pas ambiguïté, simplement $I$.
Exercice :
- Quelle doit être la taille de I si AI=A ? Même question si IA=A.
- Chercher la matrice unité de taille 1×1. Même question avec 2×2.
- Émettre une conjecture pour les matrices de taille supérieure.
- Mettre en place le produit d’une matrice A quelconque par I et expliquer pourquoi les coefficients de A sont « recopiés » dans le produit. Idem pour le produit de I par A.
2.3.6.2. Définition
On appelle matrice unité de taille $n$ la matrice carré de taille $n$ qui a des 1 sur sa diagonale principale et des 0 ailleurs.
$$ A = \begin{pmatrix} 1 & 0 & \cdots & 0 \\\\ 0 & 1 & \ddots & \vdots \\\\ \vdots & \ddots & \ddots & 0 \\\\ 0 & \cdots & 0 & 1 \end{pmatrix}$$
2.3.6.3. Propriétés et remarques
- La matrice unité commute avec toutes les matrices compatibles. En effet, $AI = IA = A$.
- Le symbole de Kronecker est un outil idéal pour manipuler ces matrices.
- En effectuant à la main un produit, on observe qu’elle a en quelque sorte un rôle de copiste. Les 0 et les 1 de $I$ laissent ou non passer les coefficients de $A$, comme des booléens (idée de masques).
2.3.7. Puissances d’une matrice
2.3.7.1. Principe
Pour que le calcul $A^2$, c’est-à-dire $A×A$, ait un sens, il faut et il suffit que $A$ soit…
De plus, comme $A^2$ et $A$ sont de même taille, on peut à nouveau les multiplier entre elles, pour obtenir $A^3$. Et ainsi de suite…
2.3.7.2. Définitions
Pour une matrice $A$ carrée de taille $n$, on définit :
- $A^0 = I$, la matrice unité de taille $n$,
- $A^1 = A$
- $A^2 = A×A$
- $A^3 = A×A×A$
- …
- $A^n = \underbrace{A×A×…×A}_{n}$
2.3.7.3. Remarques
- Pour calculer $A^3$, on utilise $A^3 = A^2×A$ ou $A^3 = A×A^2$, avec la mise en place habituelle.
- La mise en place du calcul peut serpenter. Exemples de calculs avec : $$ A = \begin{pmatrix} 1 & 1 \\\\ 1 & 0 \end{pmatrix} $$
- Mettre une matrice au carré ne revient pas à mettre tous ses coefficients au
carré. Contre-exemples :
- la matrice précédente,
- ou les matrices ne contenant que des 1, et non réduites à un coefficient.
- Les puissances de $I$ valent $I$.
- Les puissances de $A$ commutent avec $A$.
