Probabilités conditionnelles et indépendance
1. Notations
On note $E$ un univers fini et $P$ une loi de probabilité sur $E$.
On rappellera brièvement ce que sont :
- le complémentaire d’un évènement,
- l’union et l’intersection de deux évènements,
- deux évènements disjoints (ou incompatibles),
et comment on compte les éléments d’une union.
2. Probabilités conditionnelles
2.1. Quelques modes de représentation
On considère la situation décrite dans l'exemple du livre à la page 364.
2.1.1. Tableau
Souvent le plus efficace, mais le moins visuel.
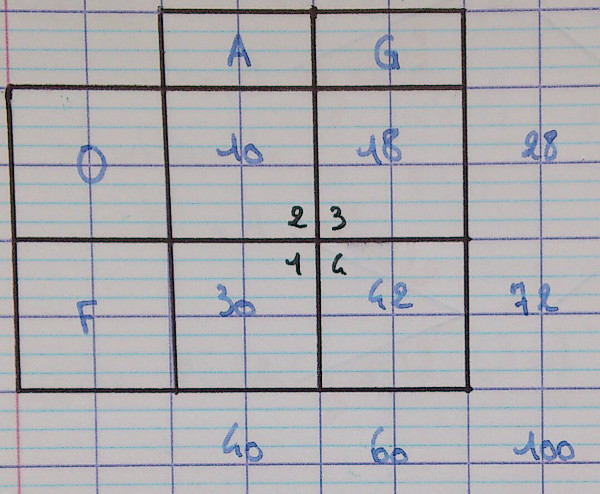
Souvent, on se contente d'une lettre pour deux ensembles : $G = \overline A$ et $F = \overline O$.
On remarque que les sommes n'apportent pas d'information nouvelle à partir du moment où l'on a la valeur des quatre cases principales, ici numérotées de 1 à 4.
Question sur ce tableau
- Combien vaut la somme des nombres des quatres cases principales ?
Que peut-on en conclure en termes de probabilités ? - Mêmes questions en prenant les cases par deux, verticalement puis horizontalement.
- Quelle est la part de bonbons à la fraise parmi les guimauves ?
2.1.2. Bulles
Le terme scientifique est diagramme de Venn.

Où se trouvent les quatres zones à numéroter de 1 à 4 ?
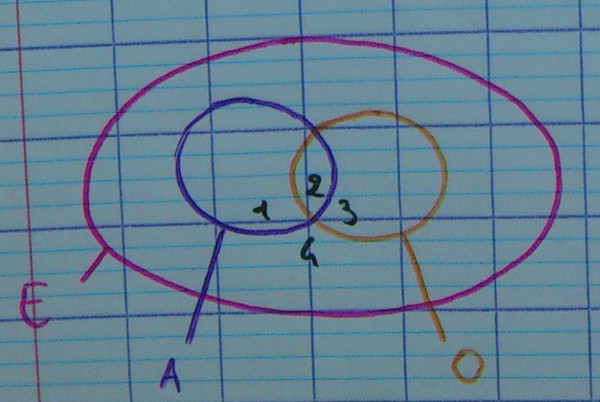
- acidulés mais pas à l'orange, c'est-à-dire acidulés à la fraise
- acidulés à l'orange
- à l'orange, mais pas acidulés, c'est-à-dire guimauves à l'orange
- ni acidulés, ni à l'orange, c'est-à-dire guimauves à la fraise
2.1.3. Bulles 2

Où se trouvent les quatres zones à numéroter de 1 à 4 ?
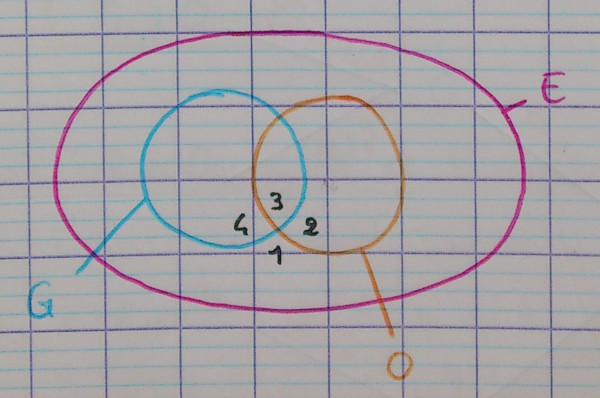
2.1.4. Autres bulles
Combien y a-t-il de façons de choisir les bulles ?
Question sur les bulles
Dans chaque diagramme à bulle, comment visualiser la part de bonbons à la fraise parmi les guimauves ?
2.1.5. Rectangles
C'est une représentation qui combine le tableau et les bulles. L'aire de chaque zone (souvent rectangle) est proportionnelle à la probabilité de l'évènement correspondant. Comme les bulles, on peut commencer par l'un ou l'autre des évènements principaux, mais la symétrie du diagramme fait qu'il y a moins de possibilités.
Questions sur les rectangles
- Quel diagramme nous permet de bien voir la part des bonbons à la fraise parmi les guimauves ?
- Dans notre exemple, peut-on faire en sorte que $A$ et $O$ soient des rectangles ?
2.1.6. Arbre pondéré
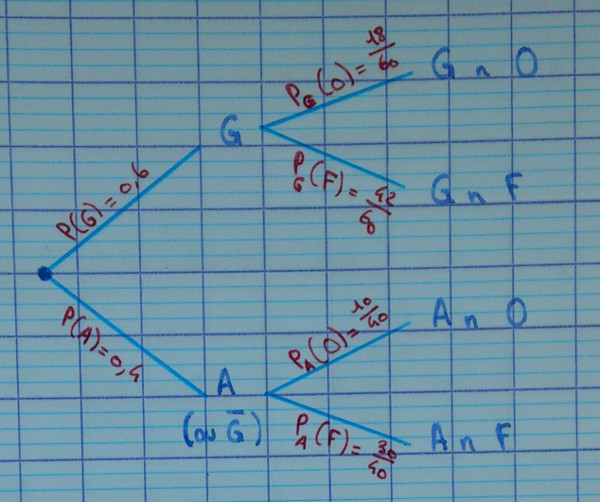
Numéroter les feuilles de 1 à 4.
Remarque : on admet que l'on multiplie les probabilités pour avancer de branche en branche. C'est ce qu'on appelle la formule des probabilités composées.
2.1.7. Arbre 2
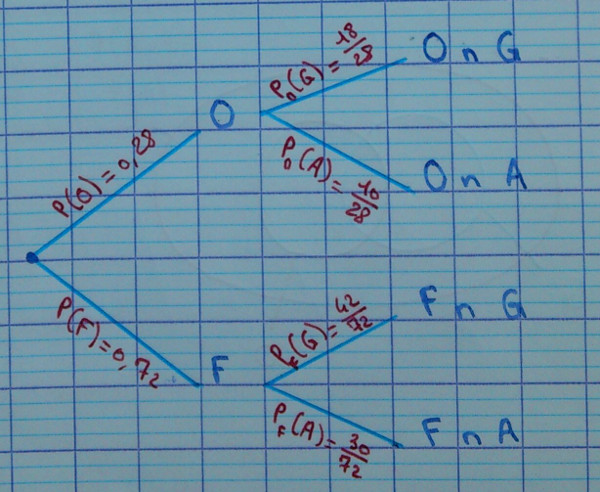
Après avoir passé une branche, on considère que l'évènement correspondant est réalisé.
Numéroter les feuilles de 1 à 4.
2.1.8. Autres arbres
Combien y a-t-il de façons de faire un abre pour cette situation ?
Lesquelles peuvent être considérées équivalentes ?
2.1.9. Question sur les arbres
Dans chaque arbre, comment visualiser la part de bonbons à la fraise parmi les guimauves ?
2.2. Définition
Soit $A$ et $B$ deux évènements avec $P(A) \ne 0$. La probabilité que $B$ se réalise sachant que $A$ est réalisé est notée $P_A(B)$ et est définie par :
$$P_A(B) = \frac{P(A \cap B)}{P(A)}$$
2.2.1. Exemple
En reprenant la question de la la part de bonbons à la fraise parmi les guimauves :
$$P_G(F) = \frac{P(G \cap F)}{P(G)} = …$$
2.2.2. Remarques
- On dira parfois tout simplement « probabilité de $B$ sachant $A$ », et on conseille d'écrire dans ce cas le $A$ après le $B$.
- On retrouve : $P(A \cap B) = P(A) × P_A(B)$ (formule des probabilités composées).
- Comme il y a deux façons d'arriver à $A \cap B$ (d'abord $A$ puis $B$ ou
d'abord $B$ puis $A$), on a :
$P(A \cap B) = P(A) × P_A(B) = P(B) × P_B(A)$.
Un exercice classique sera de passer d'une façon à l'autre. - Cette définition est liée à la multiplication de branche en branche que l'on effectue dans les arbres. On voit ici qu'il suffit diviser les membres par $P(G)$ pour retrouver la définition.
$$ \begin{aligned} P(G \cap F) &= P(G)×P_G(F) \\\\ \frac{P(G \cap F)}{P(G)} = P_G(F) \end{aligned} $$
2.2.3. Vocabulaire
« dont » « parmi » « on tire parmi » sont autant d'indices qui poussent à utiliser les probabilités conditionnelles (« sachant »).
Mais parfois, le « sachant » se cache. Expliquer en quoi cette phrase est liée à ce chapitre :
100% des gagnants ont tenté leur chance.
3. Indépendance
3.1. Définition
Deux évènements $A$ et $B$ sont dits indépendants si l'une des égalités suivantes est vraie.
- $P_B(A) = P(A)~(\text{avec}~P(A) \ne 0)$
- $P_A(B) = P(B)~(\text{avec}~P(B) \ne 0)$
- $P(A \cap B) = P(A) × P(B)$
3.2. Remarques
- L'indépendance de $A$ et $B$ revient à dire :
- « que l'on sache que $B$ soit réalisé ou que l'on ne le sache pas, la probabilité de $A$ est la même »
- « que l'on sache que $A$ soit réalisé ou que l'on ne le sache pas, la probabilité de $B$ est la même »
- Nous démontrerons plus loin que savoir si $A$ est réalisé ou non revient à savoir si $\overline A$ est réalisé ou non.
- On peut passer aisément d'une égalité à une autre. Comment ?
Schéma.
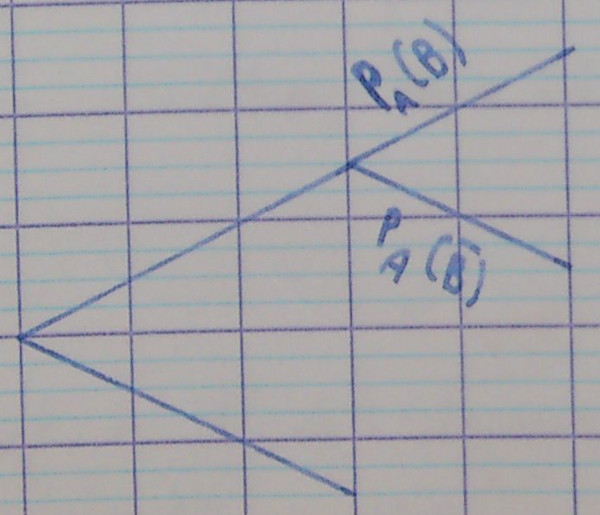
4. Avec les complémentaires
4.1. Branches d'un même nœud
La somme des probabilités des branches partant d'un même nœud vaut 1.
Autrement dit, dans l'arbre suivant, $P_A\left(B\right) + P_A\left(\overline B\right) = 1$.
4.2. Probabilités totales
4.2.1. Cas général
Le cas général est présenté ici à titre culturel. Seul le cas particulier est vraiment au programme.
Autrement dit, si :
- $\underset{1 \le i \le n}{\cup} A_i = E$
- si $i e j$, alors $A_i \cap A_j = \emptyset$
Si une famille d'évènements $(A_i)_{1 \le i \le n}$ est une partition de l'univers, alors les $(B \cap A_i)_{1 \le i \le n}$ forment une partition de $B$.
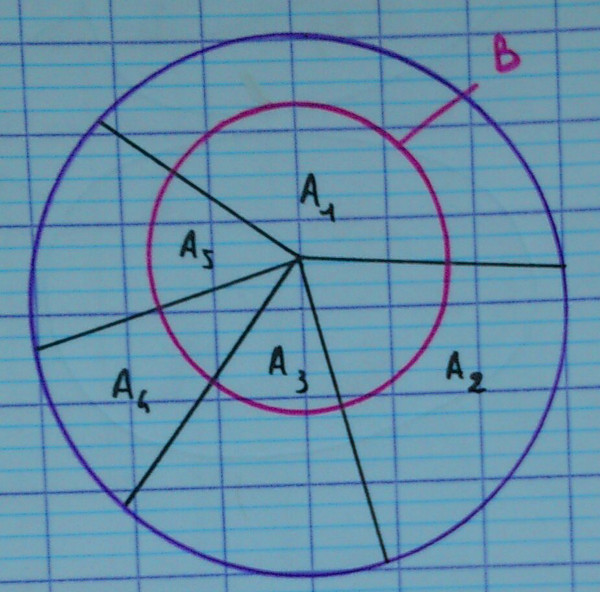
Autrement dit, on a l'union disjointe suivante :
$$B = (B \cap A_1) \cup (B \cap A_2) \cup … \cup (B \cap A_n)$$
On a donc, en termes de probabilités (puisque l'union est disjointe) :
$$P(B) = P(B \cap A_1) + P(B \cap A_2) + … + P(B \cap A_n)$$
C'est la formule des probabilités totales.
4.2.2. Cas particulier
Si $A$ est un évènement, $A$ et $\overline A$ forment une partition de l'univers. On a donc :
$$P\left(B\right) = P\left(B \cap A\right) + P\left(B \cap \overline A\right)$$
On voit ici que $B$ est constitué de :
- $B \cap A$ en bleu,
- $B \cap \overline A$ en rouge.
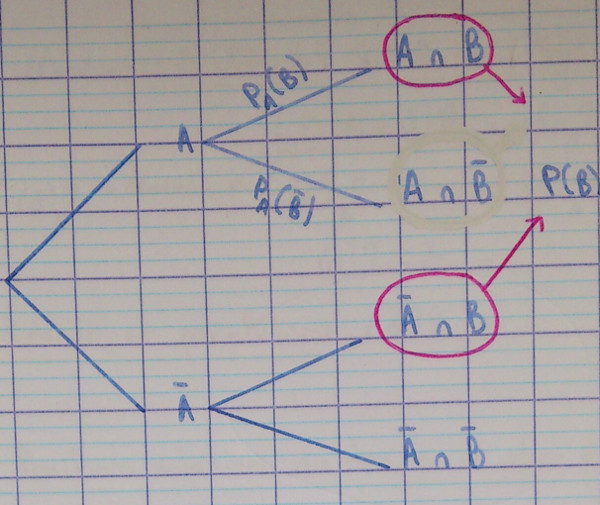
S'entraîner avec $C$ et $\overline A$ à la place de $A$ et $B$.
4.2.3. Utilisation
C'est l'incarnation la plus fréquente de la formule des probabilités totales en terminale S. Elle nous permet en quelque sorte de « retourner » l'arbre des probabilités :
$$ \begin{aligned} P(B) &= P(A \cap B) &+ &P(\overline A \cap B) \\\\ &= P(A) × P_A(B) &+ &P(\overline A) × P_{\overline A}(B) \end{aligned} $$
Ceci nous permet de construire l’autre arbre puisque nous avons $P(B)$, donc $P(\overline B)$, puis $P_B(A)$ et $P_B(\overline A)$ ainsi que $P(\overline B)$, puis $P_{\overline B}(A)$ et $P_{\overline B}(\overline A)$.
4.3. Indépendance et complémentaires
4.3.1. Propriété
4.3.1.1. Énoncé
$A$ et $B$ sont indépendants si et seulement si $\overline A$ et $B$ le sont.
4.3.1.2. Démonstration
$A$ et $B$ sont indépendants si et seulement si :
$$ \begin{aligned} P_B(A) &= P(A) &(1) \\\\ 1 - P_B(\overline A) &= P(A) &(2) \\\\ 1 - P(A) &= P_B(\overline A) &(3) \\\\ P(\overline A) &= P_B(\overline A) &(4) \end{aligned} $$
- Définition.
- La somme des probas des branches partant d'un même nœud vaut 1, soit ici $P_B(A) + P_B(\overline A) = 1$.
- On échange quelques termes de membre.
- Formule du complémentaire, voire du complémentaire du complémentaire.
Voir aussi la démonstration dans le livre à la page 368.
4.3.1.3. Remarques
- On peut décliner cette propriété. Montrer que $A$ et $B$ sont indépendants
si et seulement si :
- $A$ et $\overline B$ le sont,
- $\overline A$ et $\overline B$ le sont,
- $P_A(B) = P_{\overline A}(B)$ (on note que le complémentaire est ici en indice, pour la démonstration, passer par $P(B)$),
- …
- C'est cette dernière égalité qui nous permet de justifier que, sur la
représentation en arbre pondéré, $A$ et $B$ sont indépendants si
et seulement si les sous-arbres sont identiques.
On peut donc l’utiliser en exercice : pour affirmer qu’il y a indépendance, il suffit de dire que les sous-arbres sont identiques.
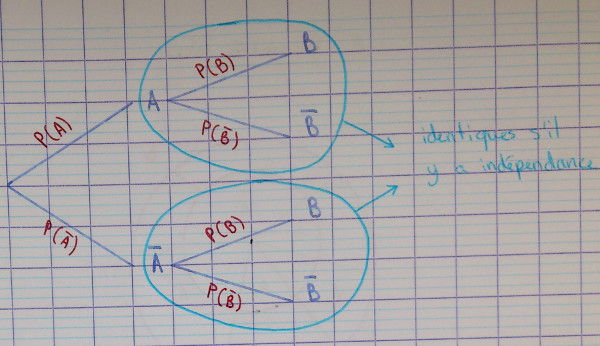
En effet, en considérant un arbre commençant par $A$ ou $\overline A$, l'indépendance de $A$ et $B$ peut être caractérisée par $P_A(B) = P_{\overline A}(B)$ ou $P_A(\overline B) = P_{\overline A}(\overline B)$. - Sur la représentation en rectangles, dans le cas où $A$ et $B$ sont
indépendants, on peut représenter $A$ ainsi que
$B$ par un seul rectangle dans le même schéma.
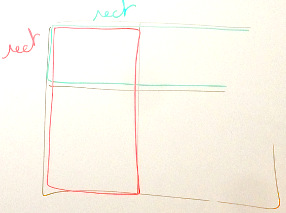
On a :
$$ \begin{aligned} P_B(A) &= \frac{\mathcal A_1}{\mathcal A_{1 \cup 2}} \\\\ P_{\overline B}(A) &= \frac{\mathcal A_3}{\mathcal A_{3 \cup 3}} \\\\ P(A) &= \frac{\mathcal A_{1 \cup 3}}{\mathcal A_{1 \cup 2 \cup 3 \cup 4}} \\\\ \end{aligned} $$
D'où l'alignement vertical, puisque le rapport dans $B$ est le même que dans $\overline B$ et que dans $E$. En effet, $P_B(A) = P_{\overline B}(A) = P(A)$.
De même :
$$ \begin{aligned} P_A(B) &= \frac{\mathcal A_1}{\mathcal A_{1 \cup 3}} \\\\ P_{\overline A}(B) &= \frac{\mathcal A_2}{\mathcal A_{2 \cup 4}} \\\\ P(B) &= \frac{\mathcal A_{1 \cup 2}}{\mathcal A_{1 \cup 2 \cup 3 \cup 4}} \\\\ \end{aligned} $$
D'où l'alignement horizontal.
En français, on peut dire :
- La proportion de $A$ et de $\overline A$ est la même que l'on soit dans $B$, dans $\overline B$ ou dans tout l'univers $E$.
- La proportion de $B$ et de $\overline B$ est la même que l'on soit dans $A$, dans $\overline A$ ou dans tout l'univers $E$.
4.3.2. Liste des caractérisations
$A$ et $B$ sont indépendants si et seulement si :
- $A$ et $B$ sont indépendants :
- $P_A\left(B\right) = P\left(B\right) $
- $P_B\left(A\right) = P\left(A\right) $
- $P\left(A \cap B\right) = P\left(A\right) P\left(B\right) $
- $A$ et $\overline B$ sont indépendants :
- $P_A\left(\overline B\right) = P\left(\overline B\right) $
- $P_{\overline B}\left(A\right) = P\left(A\right) $
- $P\left(A \cap \overline B\right) = P\left(A\right) P\left(\overline B\right) $
- $\overline A$ et $B$ sont indépendants :
- $P_{\overline A}\left(B\right) = P\left(B\right) $
- $P_B\left(\overline A\right) = P\left(\overline A\right) $
- $P\left(\overline A \cap B\right) = P\left(\overline A\right) P\left(B\right) $
- $\overline A$ et $\overline B$ sont indépendants :
- $P_{\overline A}\left(\overline B\right) = P\left(\overline B\right) $
- $P_{\overline B}\left(\overline A\right) = P\left(\overline A\right) $
- $P\left(\overline A \cap \overline B\right) = P\left(\overline A\right) P\left(\overline B\right) $
5. Rappels sur les variables aléatoires
5.1. Définition
Une variable aléatoire est un nombre $X$ associé à une expérience aléatoire. $X$ fournit donc des nombres au hasard en suivant une loi de probabilités.
5.2. Exemples
Avec un dé à six faces :
| $k$ | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| $P(X=k)$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
En comptant le nombre de « pile » sur deux tirages à pile ou face :
| $k$ | 0 | 1 | 2 | |
|---|---|---|---|---|
| $P(X=k)$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
5.3. Espérance
L’espérance d’une variable aléatoire, souvent notée $E$, est la valeur théorique que $X$ prendrait en moyenne. $E$ mesure la position de $X$.
En notant :
- $M$ la moyenne des valeurs observées après $N$ tirages,
- $x_i$ les valeurs des $N$ tirages,
- $k_j$ les différentes valeurs de $X$ possibles,
- $n_j$ les différentes valeurs de $X$ possibles,
on a :
$ \begin{aligned} M &= \frac{x_1 + x_2 + x_3 + … + x_N}{N} \\\\ &= \frac{1}{N} \left( k_1 n_1 + k_2 n_2 + k_3 n_3 + k_N n_N \right) \\\\ &= k_1 \frac{n_1}{N} + k_2 \frac{n_2}{N} + k_3 \frac{n_3}{N} + … + k_N \frac{n_N}{N} \\\\ E &= k_1 P(X=k_1) + k_2 P(X=k_2) + k_3 P(X=k_3) + … + k_N P(X=k_N) \end{aligned} $
Pour le dé :
$ \begin{aligned} E &= 1 P(X=k_1) + 2 P(X=k_2) + 3 P(X=k_3) + 4 P(X=k_4) + 5 P(X=k_5) + 6 P(X=k_6) \\\\ &= 1 \frac{1}{6} + 2 \frac{1}{6} + 3 \frac{1}{6} + 4 \frac{1}{6} + 5 \frac{1}{6} + 6 \frac{1}{6} \\\\ &= … = 3,5 \end{aligned} $
Pour les deux pièces :
$ \begin{aligned} E &= 0 P(X=0) + 1 P(X=1) + 2 P(X=2) \\\\ &= 0 \frac{1}{4} + 1 \frac{1}{2} + 2 \frac{1}{4} \\\\ &= … = 1 \end{aligned} $
5.4. Variance et écart-type
$V$ est l’espérance de $(X-E)^2$. Elle mesure la dispersion de $X$.
$ \begin{aligned} V &= (k_1-E)^2 P(X=k_1) + (k_2-E)^2 P(X=k_2) + (k_3-E)^2 P(X=k_3) + … + (k_N-E)^2 P(X=k_N) \end{aligned} $
Son unité est celle de $X$ au carré. Pour revenir à une unité raisonnable, on prend la racine carrée. C’est l’écart-type : $\sigma = \sqrt V$.
Pour le dé, $V$ vaut environ 2,9 et $\sigma$ environ 1,7.
Pour les pièces…
6. Rappels sur la loi binomiale
6.1. Épreuve de Bernoulli
6.1.1. Définition
On appelle épreuve de Bernoulli toute expérience aléatoire dont l’univers ne compte que deux issues.
6.1.2. Remarques
- Traditionnellement, ces issues sont appelées « succès » et « échec », même si la situation décrite n’a rien à voir.
- Traditionnellement, la probabilité du succès est notée $p$. $p$ est appelé le paramètre de la loi. La probabilité de l’échec est notée $q$.
- On a $q = 1-p$ et $p = 1-q$.
- Si $X$ suit une loi de probabilité de Bernoulli, ou plus simplement une loi de Bernoulli, alors on a le tableau suivant :
| $x$ | 1 | 0 |
|---|---|---|
| $P(X=x)$ | $p$ | $q$ |
6.1.3. Espérance et variance
On a $E=p$ et $V=p(1-p)=pq$. À vous de le vérifier.
6.2. Schéma de Bernoulli et loi binomiale
6.2.1. Définitions
On appelle schéma de Bernoulli de paramètres $n$ et $p$ la répétition de $n$ mêmes expériences de Bernoulli indépendantes de paramètre $p$.
En notant $X$ le nombre de succès obtenus, on définit une variable aléatoire qui suit la loi binomiale de paramètres $n$ et $p$. Cette loi est notée $\mathcal B(n,p)$.
Pour $k$ entier de 0 à $n$, on a :
$$P(X=k) = \dbinom{n}{k} p^n (1-p)^{n-k}$$
6.2.2. Remarque
- Le mot « binomiale » vient des coefficients du développement de $(a+b)^n$, qui est un binôme à la puissance $n$.
6.2.3. Quelques cas simples
6.2.3.1. Un tirage
Le cas $n=1$ correspond à une épreuve de Bernoulli, étudiée plus haut.
La loi binomiale de paramètres 1 et $p$ est tout simplement la loi de Bernoulli.
6.2.3.2. Deux tirages
Étudions $\mathcal B(2,p)$.
- Faire un arbre.
- Mettre $SS$, $EE, $SE$ et $ES$ au bout des feuilles.
- Mettre $X=0$, $X=1$ et $X=2$ juste à droite.
- Établir le tableau de la loi $\mathcal B(2,p)$.

6.2.3.3. Trois tirages
Étudions $\mathcal B(3,p)$.
Idem, en remplaçant le tableau par la donnée de $P(X=k)$ pour $k$ de 0 à 3.
6.2.3.4. Quatre tirages
Étudions $\mathcal B(4,p)$.
Idem. Écrire les différentes possibilités d’enchaînements de $S$ et de $E$. Combien y en a-t-il ?
6.2.3.5. Cas général
En notant $\dbinom{n}{k}$ le nombre de façons de choisir $k$ éléments parmi $n$, on a bien :
$$P(X=k) = \dbinom{n}{k} p^n (1-p)^{n-k}$$
Notez quelques valeurs simples de $\dbinom{n}{k}$, leur symétrie et leur somme :
- $\dbinom{n}{0} = \dbinom{n}{n} = 1$
- $\dbinom{n}{1} = \dbinom{n}{n-1} = n$
- $\dbinom{n}{k} = \dbinom{n}{n-k}$
- La somme des coefficients vaut $2^n$ (le nombre de feuilles de l’arbre).
Avec la calculatrice, pour calculer $\dbinom{4}{2} = 6$ :
- Texas Instruments :
4MathsPRBnCr2 - Casio :
4MathsOPTNnCr2
6.2.4. Espérance et variance
On a $E = np$ et $V = np(1-p)$.
On remarque que ces valeurs sont le produit par $n$ des valeurs de la loi de Bernoulli.
A suivre...
