1. Unité d’aire

1.1. Définition

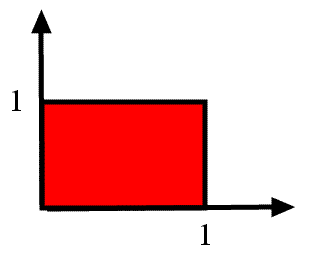
En mathématiques, une unité d’aire (U.A.) est l’aire du rectangle OIAJ où O(0;0), I(1;0), A(1;1) et J(0;1).

1.2. Conversions

Connaissant la longueur des unités de chaque axe, on peut calculer l’aire réelle d’une unité d’aire. Il suffit de les multiplier.

1.3. Exemples

• Si l’unité mesure 10 cm sur chaque axe, 1 U.A. vaut…
• Si l’unité sur l’axe des abscisses mesure 5 cm et l’unité sur l’axe des ordonnées mesure 1 cm, 1 U.A. vaut…
• Si 1 cm représente 0,1 sur l’axe des ordonnées et 2 cm représentent une unité sur l’axe des abscisses, 1 U.A. vaut…
• Si 2 cm représente 5 sur l’axe des abscisses et 3 cm représentent 20 unités sur l’axe des abscisses, 1 U.A. vaut…

1.4. Remarques

• Pour les unités d’aire (respectivement de volume), le « carré » (respectivement le « cube ») ne concernent que l’unité, et non la valeur.
  Par exemple, 10 cm²≠(10 cm)².
• Dans certains problèmes concrets, on peut ne pas avoir d’unités de longueur sur les axes. On peut par exemple mesurer :
  • le temps en secondes sur l’axe des abscisses, et de l’argent en dollars sur l’axe des ordonnées. L’unité d’aire sera en dollar.seconde.
  • le temps en heures sur l’axe des abscisses, et la puissance en watts sur l’axe des ordonnées. L’unité d’aire sera en watt.heure.

2. Intégrale

2.1. Intégrale d’une fonction positive

2.1.1. Définition

Soit $f$ une fonction continue et positive sur un intervalle $\left[a;b\right]$.

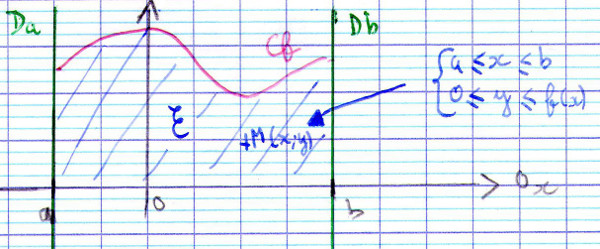
On note $\int_a^b f(x)~dx$ l’intégrale de $f$ sur $\left[a;b\right]$. C’est la valeur de l’aire en U.A. de la partie $\mathscr E$ du plan délimitée (attention chorégraphie) :

• en haut par la courbe représentative $\mathscr C_f$ d’équation $y=f(x)$,
• en bas par l’axe des abscisses $\left(Ox\right)$ d’équation $y=0$,
• à gauche par $\mathscr D_a$ d’équation $x=a$,
• à droite par $\mathscr D_b$ d’équation $x=b$.

On prononce :

intégrale de $a$ à $b$ de $f$ de $x$ $dx$.

2.1.2. Remarques

• C’est un nombre et non une aire, un peu comme 2×3 qui est avant tout le nombre 6 alors que 6 U.A. est l’aire d’un rectangle de côtés 2 et 3.
• On dit aussi parfois : « somme de $a$ à $b$ de $f$ de $x$ $dx$ ».
• On parlera souvent « d’aire sous la courbe ».
• $a$ et $b$ sont appelées les bornes d’intégration.
• $x$ est la variable d’intégration. Elle est muette.
  
  On note indifféremment $\int_a^b f(x)~dx$ ou $\int_a^b f(t)~dt$, de la même façon que l’on définit indifféremment la fonction carré par $g(x)=x^2$ ou $g(t)=t^2$.
• Si $a=b$, on a $\int_a^b f(x)~dx = ...$.
  $\int_a^b f(x)~dx = 0$

2.2. Intégrale d’une fonction non positive

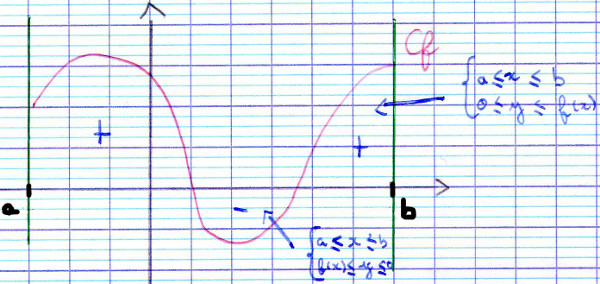
On étend la définition aux fonctions non positives : si la fonction $f$ change de signe, les aires des zones où $f$ est négative sont comptées négativement.

2.3. Sens des bornes

On étend la définition aux bornes inversées : si $a > b$,

$$\int_a^b f(x)~dx = -\int_b^a f(x)~dx$$

Bien sûr, cette égalité peut être lue dans les deux sens.

Exemple : Calculer $\int_2^0 x~dx$.

3. Propriétés de l’intégrale

3.1. Relation de Chasles

Pour tout $a$, $b$ et $c$ de l’intervalle $I$, $$\int_a^b f(x)~dx + \int_b^c f(x)~dx = \int_a^c f(x)~dx$$

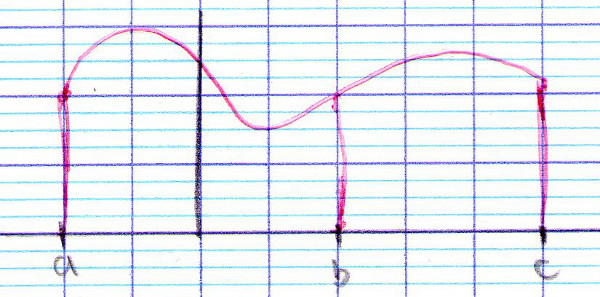
Égalité qui reste valable si $f$ n’est pas positive ou si les bornes ne sont pas ordonnées de façon croissante.

En particulier, on a : $$\int_a^b f(x)~dx + \int_b^a f(x)~dx = \int_a^a f(x)~dx = 0$$

3.2. Linéarité de l’intégrale

Soit $f$ et $g$ deux fonctions continues sur $I$ et $k$ est un nombre réel. Pour $a$ et $b$ dans $I$, on a :

• $\int_a^b k×f(x)~dx = k × \int_a^b f(x)~dx$ (noter le cas où $k = -1$)
• $\int_a^b \left(f(x)+g(x)\right)~dx = \int_a^b f(x)~dx + \int_a^b g(x)~dx$

Autrement dit :

• l’intégrale du produit par une constante est égale au produit par une constante de cette intégrale ;
• l’intégrale d’une somme est égale à la somme des intégrales.

Voir figures et démonstrations dans le livre.

3.3. Positivité de l’intégrale

Ces propriétés sont expliquées ou démontrées p.248 du livre.

3.3.1. Positivité

Si $a \le b$ et si pour tout $x$ de $\left]a;b\right[$ on a $f(x) \ge 0$, alors $\int_a^b f(x)~dx \ge 0$.

3.3.2. Comparaison

Si $a \le b$ et si pour tout $x$ de $\left]a;b\right[$ on a $f(x) \le g(x)$, alors $\int_a^b f(x)~dx \le \int_a^b g(x)~dx$.

3.3.3. Minoration ou majoration

Si $a \le b$ et si pour tout $x$ de $\left]a;b\right[$ on a $m \le f(x) \le M$, alors $m(b-a) \le \int_a^b f(x)~dx \le M(b-a)$.

4. Calcul d’intégrales

4.1. À la main

Si les zones « sous la courbe » ont des formes géométriques simples (rectangles, triangles, trapèzes, demi-disques…) alors peut utiliser les formules d’aire correspondantes.

Rappels :

• rectangles : $L×l$
• triangles : $\frac{1}{2}×B×h$
• trapèzes : $\frac{1}{2}×(b+B)×h$
• disques : $\pi r^2$

4.2. Avec les primitives

A suivre...