Méthode d’Euler pour l’exponentielle
1. Le problème
On cherche à résoudre l’équation différentielle (E): $f'=f$.
Autrement dit, on cherche une fonction dérivable qui est sa propre dérivée.
Ce problème peut paraître totalement artificiel et purement intellectuel, mais la nature, qui aime les choses simples, le propose aux plantes et aux animaux.
Exemples :
- tour sous contrainte poids homogène,
- amorti de température, de charge électrique ou de radioactivité,
- spirales logarithmiques,
- amorti de sinusoïdes,
- liens avec la trigonométrie et les nombres complexes,
- chaînette,
- …
2. Partie théorique
2.1. Solution triviale
Soit $f$ la fonction nulle, c’est-à-dire définie pour tout $x$ réel par $f(x) = 0$. Montrer que $f$ est solution de l’équation (E).
2.2. Solutions polynômiales
Soit $f$ une fonction polynôme de degré $n$ et $g$ la fonction définie sur $\mathbb R$ par $g(x) = f(x) - f'(x)$. On suppose qu’on a écrit $f$ ainsi, avec $a_n \ne 0$ : $$ f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_2 x^2 + a_1 x + a_0 $$ Donner l’expression de $g$.
Nous allons maintenant supposer que $f$ est solution de (E).
- Que dire de la fonction $g$ si $f$ est solution de (E) ?
- Expliquer la contradiction au niveau du coefficient $a_n$.
- Un polynôme peut-il être une solution de (E) ?
2.3. Infinité potentielle de solutions
Soit $f$ une solution de (E) sur $\mathbb R$ et $k$ un nombre réel. Montrer que toute fonction $g_k$ définie sur $\mathbb R$ par $g_k(x) = k×f(x)$ est solution de (E).
Si $f$ n’est pas la fonction nulle et si $k$ n’est pas nul, c’est le jackpot !
3. Partie pratique
On suppose dans cette partie qu’il existe une fonction $f$ vérifiant (E) et telle que $f(0)=1$. Soit $h$ un nombre réel strictement positif.
Nous allons appliquer la méthode d’Euler, qui consiste à dire :
Autour de l’un de ses points, une courbe représentant une fonction assez régulière est proche de la tangente à la courbe en ce point.
3.1. Partie théorique de la partie pratique
3.1.1. Premier point
On note $M_0$ le point de $C_f$ d’abscisse $0$ ($0×h$). Donner son ordonnée et placer $M_0$ dans un repère.
3.1.2. Cas h=0,5
3.1.2.1. Deuxième point
On note $M_1$ le point de $C_f$ d’abscisse $h$ ($1×h$).
Comme on ne connait pas $f$, on ne connait pas $f(h)$, mais on va l’approcher par l’ordonnée de $N_1$, le point de la tangente à $C_f$ en $M_0$ qui a la même abscisse.
- Donner $f'(0)$ puis l’équation de la tangente à $C_f$ en $M_0$, notée $T_1$.
- En déduire l’ordonnée du point $N_1$.
3.1.2.2. Troisième point
En supposant que $N_1$ approche assez bien $M_1$, on suppose qu’il se trouve sur $C_f$, déterminer une équation de la tangente à $C_f$ en $M_1$, notée $T_2$, puis en déduire l’ordonnée du point $N_2$.
3.1.3. Cas général
On rappelle que $N_n$ est le point d’abscisse $n×h$ qui approche $M_n(n×h, f(n×h))$. On note $u_n$ l’ordonnée de $N_n$.
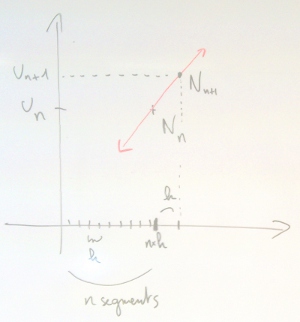
3.1.3.1. Expression récursive
En appliquant la méthode d’Euler, donner l’expression de $u_{n+1}$ en fonction de $u_n$ et $h$.
Quel type de suite reconnaît-on ?
En déduire la valeur de $u_n$ de façon explicite (sans utiliser le terme précédent).
3.1.3.2. Sens de l’approche
De quel côté approche-t-on la courbe ?
- sur $\left[0;+\infty\right[$
- sur $\left]-\infty;0\right[$
3.2. Partie pratique de la partie pratique
3.2.1. Feuille de calcul
Construire une feuille de calcul de tableur sur le modèle ci-dessous, qui donne les coordonnées des points $N_n$.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | pour h= | 0,5 | ||
| 2 | x | y | ||
| 3 | $N_0$ | 0 | 1 | |
| 4 | $N_1$ | 0,5 | 1,5 | |
| 5 | $N_2$ | |||
| 6 | $N_3$ | |||
| 7 | $N_4$ |
3.2.2. Valeur en 1
Comment choisir $h$ pour que $N_n$ ait pour abscisse 1 ?
En faisant varier $h$, donner différentes valeurs approchées de $f(1)$. Écrire les résultats sous forme de tableau sur un deuxième onglet.
| h | f(1) |
|---|---|
Pour 0,1 c’est environ 2,294.
Pour 0,001 c’est environ 2,717.
Pour 0,001 c’est environ 2,718.
Pour 0,000001 c’est environ 2,718268.
=EXP(1) donne la valeur théorique
approchée par le tableur : 2,71828183.
En déduire la limite de $(1 + \frac{1}{n})^n$ quand $n$ tend vers l’infini.
3.2.3. Courbe représentative sur [0;1]
En utilisant les fonctionnalités graphiques du tableur, tracer $C_f$ sur $\left[0;1\right]$.
3.2.4. Courbe représentative sur [0;10]
En utilisant les fonctionnalités graphiques du tableur, tracer $C_f$ sur $\left[0;1\right]$. Que peut-on en dire ?
3.2.5. Courbe représentative sur [-1;0]
En utilisant les fonctionnalités graphiques du tableur, tracer $C_f$ sur $\left[-1;0\right]$.
