1. Le principe

1.1. Énoncé des règles à l’oral et exemple

On choisit un nombre entier positif. S’il est pair, on le divise par deux. S’il est impair, on le multiplie par 3 puis on ajoute 1 au résultat. Dans les deux cas, on applique à nouveau le procédé au dernier nombre trouvé.

Exemple avec 6. On note la suite des nombres au tableau.

1.2. Application concrète

Chaque élève choisit un nombre entre 7 et 15 inclus, puis applique le procédé en écrivant les nombres trouvés au fur et à mesure. Vérification pour quelques uns.

2. En classe

2.1. Travail demandé

Chaque élève doit expliquer le principe :

• oralement en français,
• par écrit en français,
• en dessinant un schéma de type organigramme ou flowchart,
  • exemples sur Google
  • sur Tumblr
  • un organigramme simple
  • un autre plus complexe
  • pendant ce temps, chez Nintendo
• en écrivant du pseudo-code ou même du code (qu’il peut aller tester).

2.2. Réponses possibles

2.2.1. En maths

Soit $u_0$ un entier non nul. Pour tout $n$ de $\mathbb N$, $$ \begin{aligned} u_{n+1} &= u_n / 2 &si\ n\ pair \\\\ u_{n+1} &= 3 u_n + 1 &sinon \\\\ \end{aligned} $$

2.2.2. En français

• On choisit un nombre de départ.
• Si ce nombre est pair, on en calcule la moitié,
• sinon, on calcule le triple du nombre plus un.
• Si le résultat vaut 1, on arrête,
• sinon on prend le résultat comme nouveau nombre de départ.

2.2.3. Avec un diagramme

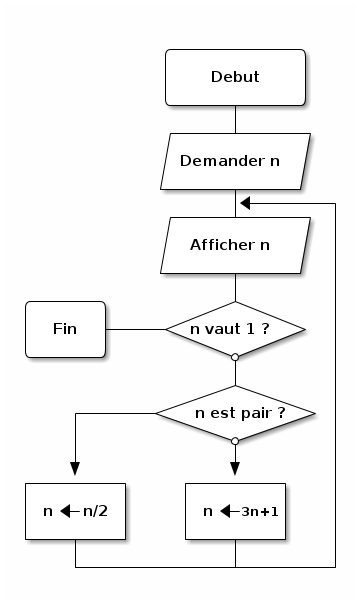
2.2.4. En pseudo-code

Demander n
Tant que n ne vaut pas 1
 |  Afficher n
 |  Si n est pair, alors
 |   |  n <- n/2
 |  Sinon
 |   |  n <- 3*n + 1
 |  Fin du Si

2.2.5. En Python

Voir le fichier squelette, qui permet de spécifier le nombre de départ.

2.3. Remarque

On remarque que le pseudo-code et le code Python ne sont pas une traduction exacte du diagramme.

3. Place de cette suite dans les mathématiques

Voir l’article sur Wikipedia.

4. Travail à la maison

Pour chaque objectif ci-dessous, créer un algorithme.

• à partir d’un entier n, le temps de vol de n,
• à partir d’un entier n, le temps de vol en altitude de n,
• à partir d’un entier n, l'altitude maximale de n.

Voir cet article Wikipedia pour le vocabulaire.

Pour chacun des algorithmes créé, vous dessinerez un organigramme et écrirez le pseudo-code.

Vous pouvez vous inspirer des éléments de réponse un peu plus haut sur cette page. Il vous suffira d’incorporer un compteur.

i <- 0      # initialisation
i <- i+1    # incrémentation
Afficher i  # affichage

Une fois que le professeur a validé l’organigramme et le pseudo-code, vous pouvez tester votre algorithme en le programmant en Python. Vous pouvez télécharger l’algorithme sans compteur programmé en Python pour vous en servir comme base. Pensez à « sauver sous » (File/Save as) un nouveau nom pour chaque fichier avant de faire des modifications.

5. Exercices complémentaires

5.1. Meilleurs dans la première centaine

Parmi les nombres compris entre 1 et 100,

• quel est celui qui a le temps de vol le plus long ?
• quel est celui qui a le temps de vol en altitude le plus long ?
• quel est celui qui a l’altitude maximale la plus haute  ?

5.2. Autres

Laissez aller votre imagination et inventez-vous vous-même un problème !