1. Sur feuille

En cours de rédaction…

2. Sur machine

2.1. Calcul de nombres congrus à un autre

2.1.1. Reste de la division euclidienne

Écrire un algorithme qui demande deux entiers n et d et qui donne le reste de la division euclidienne de n par d.

Remarque : C’est un exercice facile si on utilise l’opérateur modulo : %. Si vous le faîtes sans utiliser cet opérateur, vous aurez plus de facilité à faire l’exercice suivant.

2.1.2. Nombres congrus dans un intervalle

Écrire un algorithme qui demande quatre entiers n, d, a et b et qui donne tous les nombres congrus à n modulo d compris entre a et b.

Il est bien sûr possible de le faire par force brute, en testant chaque entier entre a et b, ou par semi force brute (trouver le premier nombre par force brute puis les autres en utilisant l’exercice précédent) mais une méthode plus mathématique sera appréciée.

2.2. Parcours de listes circulaires

Le but de cet exercice est d’observer que :

Modulo d, les multiples de n sont les multiples de pgcd(n,d).

Pour cela, nous allons simuler des listes circulaires à l’aide de tableaux et de l’opérateur % (modulo).

2.2.1. Avec 10 chiffres

Ici, pas besoin de tableau.

1. Écrire un programme qui demande un entier n à l’utilisateur et qui affiche ses dix premiers multiples (0×n, 1×n, 2×n…).
2. Écrire un programme qui demande un entier n à l’utilisateur et qui affiche le reste dans la division euclidienne par 10 de ses dix premiers multiples.
3. Écrire un programme équivalent au précédent, mais qui teste lui-même les nombres n de 1 à 20. Pour une analyse plus commode du résultat, on préfèrera afficher 20 lignes avec, sur chaque ligne, n puis les 10 nombres à un chiffre qu’il génère.

 1 : 0123456789
 2 : 0246802468
 3 : 0369258147
...
20 : 0000000000

Pour quels nombres n obtient-on les 10 chiffres ?

 1 : 0123456789 PGCD(1,10)=1
 2 : 0246802468 PGCD(2,10)=2
...
20 : 0000000000 PGCD(20,10)=10

2.2.2. Avec l’alphabet

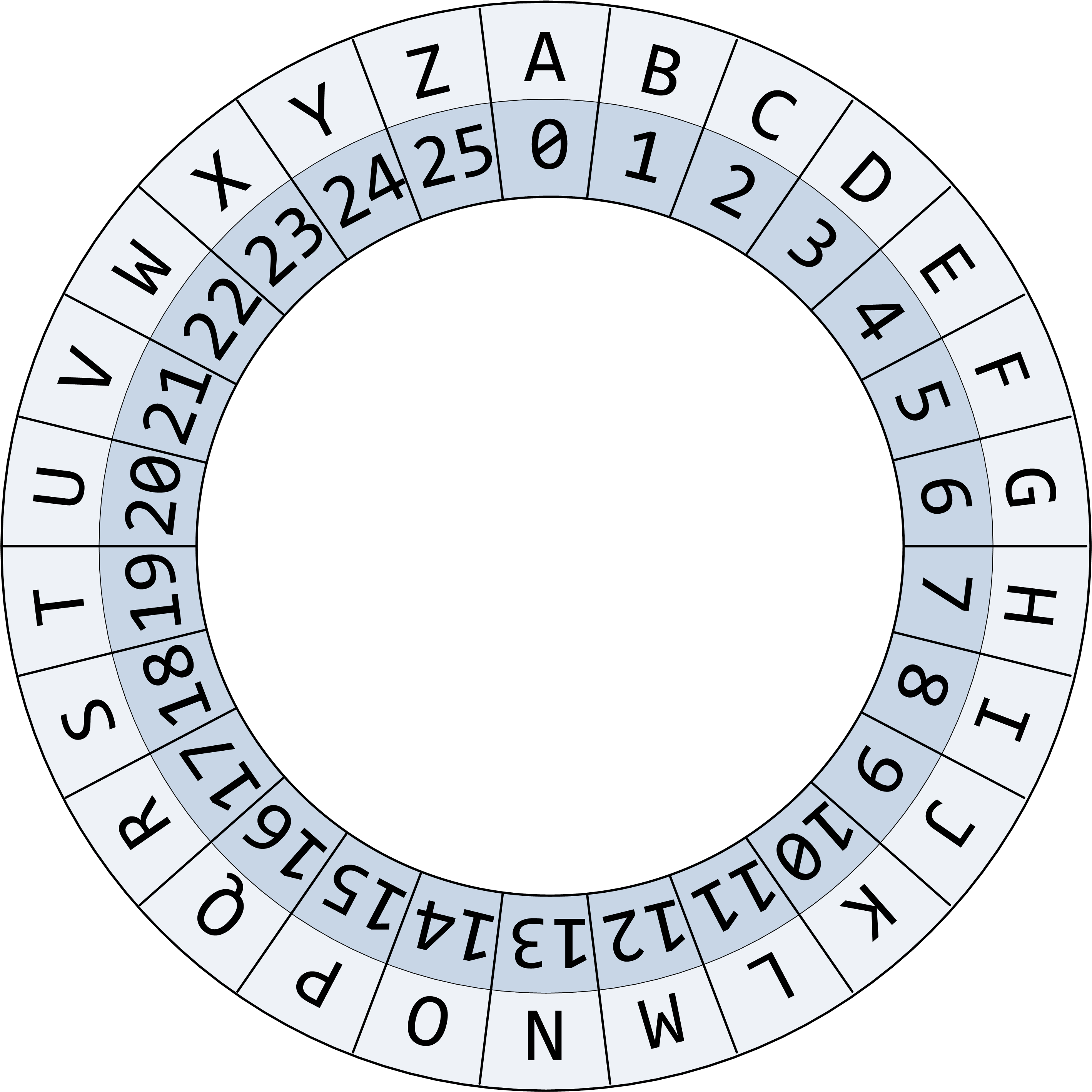
2.2.2.1. De trois en trois

Le but ici est d’afficher une lettre sur trois (A, D, G…), en recommençant au début de l’alphabet une fois arrivé à la fin (…, V, Y, B, E…) comme si l’alphabet était circulaire :
...WXYZABCD....

Questions préliminaires :

1. Pourquoi les lettres ainsi sélectionnées forment-elles un cycle ?
2. Quel est le nombre maximum de lettres possible dans un de ces cycles ? Faudra-t-il 10, 20, 50, 100 itérations ?

Programmation :

Écrire un programme qui :

• stocke les lettres de l’alphabet dans un tableau,
• affiche une lettre sur trois (A, D, G…), en recommençant au début de l’alphabet une fois arrivé à la fin, comme si l’alphabet était circulaire :
  ...WXYZABCD....

Autres questions :

1. Au bout de combien de lettres a-t-on fait un tour complet ?
2. Que se passe-t-il si on refait la même expérience avec une lettre sur deux au lieu de trois ?

2.2.2.2. Cas général

1. Écrire un programme qui demande un entier n à l’utilisateur et qui parcourt l’alphabet en sautant n lettres à chaque fois.
2. Écrire un programme équivalent au précédent, mais qui teste lui-même les nombres n de 1 à 26. Pour une analyse plus commode du résultat, on préfèrera afficher 26 lignes de 26 lettres.

ABCDEFGHIJKLMNOPQRSTUVWXYZ
ACEGIKMOQSUWYACEGIKMOQSUWY
ADG...          ...FILORUX
...
AYW...
AZYXWVUTSRQPONMLKJIHGFEDCB
AAAAAAAAAAAAAAAAAAAAAAAAAA

2.2.3. Conclusion

On notera en particulier que le parcours n’est exhaustif que quand la longueur du saut et la taille de la liste sont des entiers premiers entre eux.

3. Clés de contrôle

3.1. NIR

Parmi les codes INSEE, le plus célèbre est sûrement le NIR.

C’est un nombre à 13 chiffres suivi d’une clef de contrôle à un chiffre. Ces nombres seront notés respectivement $A$ et $K$ et leur association est considérée valides si : $$A + K \equiv 0 \left[ 97 \right]$$

1. Verifier la validité des paires $A$ et $K$ suivantes :
   • 2 55 08 14 168 025 12
   • 1 77 09 76 451 032 10
   • 2 82 12 75 114 123 14
2. Donner une clef valide pour 1 56 11 13 055 376. Est-elle unique ?
3. Pourquoi 97 ? Pourquoi pas 2 ? 10 ? 100 ? 1000 ?
4. Pour un $A$ donné, on tire un $K$ au hasard. Quelle est la probabilité que cette clef soit valide ?
5. Montrer que si un seul chiffre est erroné, l’erreur est détectée.
6. Montrer que si deux chiffres sont intervertis, l’erreur est détectée.