1. Principaux symboles

1.1. Début et Fin

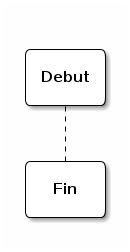
Pseudo-code :

Début algorithme MON_ALGO
...
Fin algorithme MON_ALGO

1.2. Entrées et Sorties

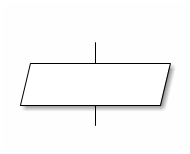
Pseudo-code :

Demander...

Afficher...

On représente ainsi toutes les intéractions avec l’extérieur.

En entrée, on a souvent une valeur ou une suite de valeurs sur laquelle l’utilisateur veut que l’ordinateur travaille (un nombre, du texte…). Cela peut aussi être une lecture dans un fichier ou une base de donnée, un périphérique de capture de son, d’image…

Voir la fonction input dans memo Python.

Les sorties peuvent être aussi très variées :

• afficher un résultat à l’écran,
• imprimer,
• écrire dans un fichier, une base de donnée,
• actionner un moteur, un haut-parleur…

1.2.1. Remarques

Les entrées et sorties sont parfois abrégées E/S en français et I/O en anglais, pour Input et Output.

Plus subtil, l’instruction Demander est parfois notée Lire (ou Read en anglais, read est encore utilisée dans certains langages, notamment les shells) et est considérée comme une lecture. De même pour ce que l’on a appellé ici Afficher, qui est parfois noté Écrire (ou Write ou Print en anglais) et qui est considéré comme une écriture.

Il faut bien comprendre que l’on se place du point de vue de l’ordinateur, ce n’est pas l’utilisateur qui lit, mais la machine ! Utiliser Saisir à la place de Demander est contradictoire avec ce point de vue.

1.2.2. Pour une meilleure interaction avec l’utilisateur

Souvent, on effectuera une écriture (affichage) du genre :

Afficher "Taper un nombre SVP: "

avant une instruction de lecture du genre :

Demander n

pour que l’utilisateur du programme sache ce qu’on lui demande.

1.3. Test

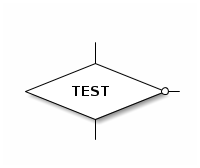
La position des branches n’a pas d’importance, seul l’emplacement du cercle compte.

Remarque mnémotechnique : Faux est souvent codé par 0.

Pseudo-code :

Si TEST, alors
 |  ...
Sinon
 |  ...
Fin Si

Pour maîtriser toute la puissance des tests, il faudra (entre autres) comprendre :

• la section sur les booléens,
• le cours sur le calcul des propositions.

En effet, un test sera réalisé en programmation par une expression booléenne qui pourra être construite à partir de connecteurs logiques.

1.4. Traitement ou sous-programme (sous-organigramme)

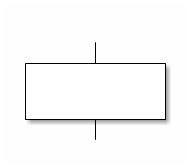
Dorénavant, quand vous verrez un tel rectangle vide ou contenant un vague « Traitement », il faudra imaginer une quelconque opération informatique élémentaire, comme une affectation, une entrée ou une sortie, et même un enchaînement de symboles comme ceux que l’on vient de voir (rectangle vide ou comprenant un vague « Traitement » compris !).

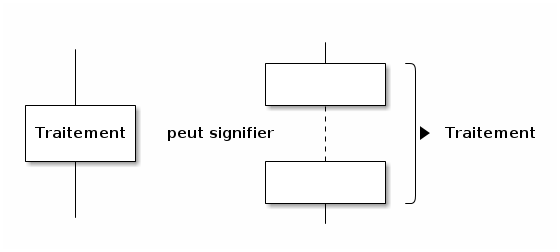
Remarque importante : On ne peut utiliser que ces symboles, et un traitement un tant soit peu complexe doit être détaillé par une combinaison de symboles élémentaires, souvent appelés primitives. On ne s’autorise pas de traitements du genre : « si le résultat est juste, on fait avec un de plus » (l’ordinateur ne sait pas si un résultat est juste ou faux) ou « on compare l’entrée utilisateur avec i » (entrée/sortie et test à la fois).

2. Principales structures

2.1. Notes sur les organigrammes et le pseudo-code

On rappelle que dans un organigramme, aucune des structures détaillées ici n’a son propre symbole. Dans un organigramme, il faudra toujours détailler un traitement non élémentaire par une ou plusieurs des structures vues ci-dessous.

En revanche, en pseudo-code, on pourra écrire Tant que…, Pour i de 1 à 10…… Cette facilité a une contrepartie : on ne peut pas utiliser une ruse graphique (accolade, flèche ou points de suspension) pour exprimer un algorithme, à part l’indentation (décalage vers la droite d’une ligne pour). Un algorithme en pseudo-code est une suite de lignes, c’est tout.

2.2. Séquence linéaire

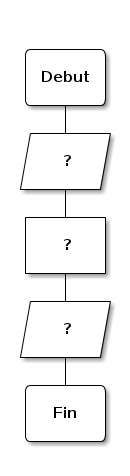
Pseudo-code :

Début algorithme MON_ALGO
...
Entrée-sortie
...
Traitement
...
Entrée-sortie
...
Fin algorithme MON_ALGO

Question : Pourquoi a-t-on choisi d’enchaîner ces trois symboles précis dans cet ordre pour ce premier exemple ?

2.3. Séquence conditionnelle

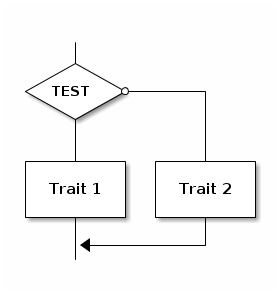
Lorsque que l’on revient sur la ligne (ou branche) d’exécution principale, on indique une flèche. Cette flèche doit pointer sur un trait entre deux symboles.

Attention, la branche principale peut correspondre à un test faux (moyen mnémotechnique : branche du zéro en sortant du losange) ou à un test vrai, suivant dans quel esprit est fait le test, ce qui est purement subjectif.

Pseudo-code :

Si TEST, alors
 |  Traitement 1
Sinon
 |  Traitement 2
Fin Si

Remarque :

Si un seul des traitements vous intéresse, il suffit de remplacer l’autre par un simple trait. L’idéal est d’adapter si besoin la condition pour que l’on n’aie pas à écrire de Sinon, comme ici :

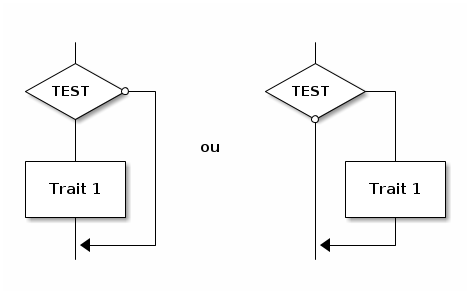
Pseudo-code :

Si TEST, alors
 |  Traitement 1
Fin Si

2.4. Tant que (, faire)

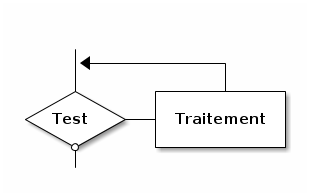
Pseudo-code :

Tant que TEST
 |  Traitement
Fin Tant que

Remarques

• Seule la condition TEST décide de l’exécution (ou de la ré-exécution) du bloc Traitement. Fin Tant que n'indique pas de fin directe après l’exécution du bloc, sauf si la condition devient fausse directement bien sûr.
  Il en sera de même pour toutes les structures de type boucle. Par exemple les boucles de type pour ne s’arrêteront au Fin Pour que si le bon nombre d’itérations a été effectué. Le mot « fin » ne signale que la fin du bloc.
• TEST peut être une combinaison de conditions (voir le cours sur le calcul des propositions).
  Exemple :

n <- 0
Tant que n² < 100 ou n est pair
 |  n <- n + 1
Fin Tant que
Afficher n

2.5. Jusqu’à ce que (, faire)

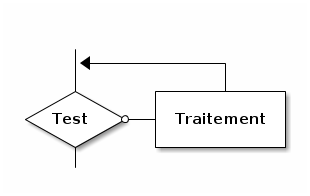
Pseudo-code :

Jusqu’à ce que TEST
 |  Traitement
Fin Jusqu’à ce que

2.6. Faire tant que

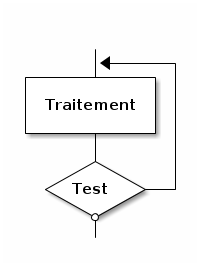
Pseudo-code :

Faire
 |  Traitement
Tant que TEST
Fin Faire tant que

Remarque :

Peu de langages possèdent les instructions qui commencent par « faire ». C’est pourtant pratique quand, par exemple, on a la séquence suivante :

1. demander une valeur à l’utilisateur,
2. vérifier que cette valeur est valide,
3. recommencer tant que la valeur n’est pas valide.

while True:
    traitement()
    if not test:
        break

2.7. Faire jusqu’à ce que

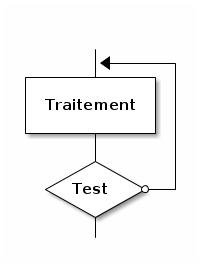
Pseudo-code :

Faire
 |  Traitement
Jusqu’à ce que TEST
Fin Faire Jusqu’à ce que

2.8. Boucles Pour

2.8.1. Avec valeur finale

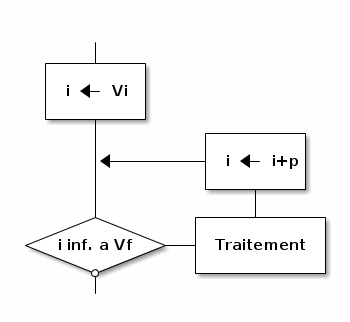
Pseudo-code :

Pour i de Vi à Vf (par pas de p), faire
 |  Traitement
Fin Pour

Ou parfois :

Pour i de Vi à Vf (par pas de p), faire
 |  Traitement
i suivant

2.8.2. Avec condition

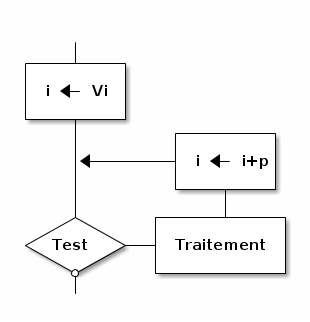
Pseudo-code :

Pour i de Vi tant que Test (par pas de p), faire
 |  Traitement
Fin Pour

2.8.3. Remarques

2.8.3.1. Variable d’itération

Le lettre i représente la variable d’itération de la boucle. On l’utilise sans doute parce que c’est la première lettre des mots index et indice, mais aussi parce qu’elle est souvent utilisée comme variable muette quand on étudie les suites en mathématiques (avec j et k). Il est souvent préférable de trouver des noms plus explicites.

La variable d’itération va prendre des valeurs différentes dans chacun des tours de la boucle. Inutile de l’incrémenter dans le corps de la boucle puisque :

• dans les langages de type C ou Java, on écrit i++ en troisième argument du for;
• en Python, la variable parcourt la liste et changera de valeur en passant d’une case à l’autre dans la liste (voir le point 5 des singularités de Python à ce sujet).

2.8.3.2. Pas

La lettre p désigne le pas de la boucle. C’est la valeur des sauts que fait la variable d’itération. Si on ne l’indique pas, il faut 1 par défaut (c’est pratique car on veut le plus souvent travailler avec des entiers consécutifs).

2.8.3.3. Divers

• La boucle pour peut toujours être mise en place par une boucle tant que.
• Les boucles de type pour ne s’arrêteront au Fin Pour que si le bon nombre d’itérations a été effectué. Le mot « fin » ne signale que la fin du bloc.

2.9. Utilisation du Sinon si et du Selon que

En cours de rédaction…

3. Premiers algorithmes

Donner l’organigramme et le pseudo-code de chacun.

3.1. Doubler l’entrée

Le programme demande un nombre entier à l’utilisateur, puis le programme affiche le double du nombre entré par l’utilisateur.

3.2. Vérifier la valeur

Le programme demande l’âge de l’utilisateur, puis le programme dit si l’utilisateur est majeur ou mineur. C’est tout.

3.3. Racines d’un polynôme du second degré

Le programme affiche «$ax^2 + bx + c$, donnez a, b et c: » puis demande trois nombres à l’utilisateur. Ensuite le programme calcule le discriminant et, suivant sa valeur, donne les éventuelles racines du polynôme (faire des recherches si vous ne savez pas ce qu’est le discriminant).

Attention, il y a trois cas à gérer. Pour vous en sortir, vous pourrez imbriquer des tests.

Vous pourrez tester votre programme sur $x^2 - 5x + 4$ en remplaçant $x$ par les racines trouvées afin de vérifier que le polynôme s’annule bien en ces valeurs.

3.4. Doubler l’entrée en boucle

Le programme répète indéfiniment l’algorithme précédent :

Le programme demande un nombre à l’utilisateur, puis le programme affiche le double du nombre entré par l’utilisateur.

mais s’arrête si l’utilisateur entre la valeur 0.