Récursivité
- Introduction
- Récursivité en informatique
1. Introduction
1.1. La récursivité est partout
La notion de récursivité est une notion essentielle, et pas seulement en en informatique. En effet, pour expliquer une situation, on utilise souvent cette même situation à un état précédent, voire, dans certains cas plus complexes, on intègre une version de cette situation dans elle-même.
1.2. Exemples généraux
Points de départ :
- L’article Wikipedia sur la récursivité, pour un point de vue général.
- Les mises en abyme se
retrouvent dans :
- les poupées russes,
- la Vache qui rit,
- les pizzas,
- les desserts
- …
- En littérature, certains textes sont conçus de façon à ce qu’ils se mordent la queue, comme Les mille et une nuits, ou En attendant Godot.
- Les acronymes récursifs.
- Les Recursive transition network.
- Les suites définies par récurrence sont bien sûr le premier exemple de récurrence en mathématiques, mais cela peut aller beaucoup plus loin puisque certaines théories mathématiques étudient les propriétés de certaines théories mathématiques.
- Les fractales sont aussi un bel
exemple de récursivité en mathématiques. Elles servent à décrire la
nature,
mais bien d’autres choses
encore,
comme l’organisation en fractale de villages en Afrique (présentation TED
de Ron Eglash).
Mais savez vous ce qu’est une fractale ?
- Le jeu des tours de Hanoï peut se résoudre de façon élégante grâce à la récursivité. Voir cette page.
- On peut trouver ce concept dans des web comics ou plus sérieusement dans des bandes dessinées ou au cinema.
- Recursive Drawing, un espace de dessin récursif, avec implémentation dans le navigateur.
- « To iterate is human, to recurse divine » - L. Peter Deutsch
- …
1.3. Définition générale
On dit qu’on définit une notion nouvelle de manière récursive lorsque cette notion fait partie de sa propre définition.
Cette manière de procéder heurte le sens commun car on a l’habitude de définir un objet en utilisant des objets connus, mais c’est pourtant le mode de pensée le plus adapté à beaucoup de problèmes.
D’une manière générale, une définition récursive doit être complétée par la connaissance d’un cas particulier au moins (le point d’appui) pour lequel on connaît explicitement le résultat, souvent trivial.
2. Récursivité en informatique
VP : c’est marrant
CR : c’est pas hyper bien
2.1. Fonctions ou procédures
2.1.1. Sur des exemples
2.1.1.1. Un exemple trivial
Que fait ce programme ?
def boucle():
print("je boucle")
boucle()
boucle()
2.1.1.2. Factorielle
2.1.1.2.1. Définition
On définit la factorielle d’un entier naturel par $n! = 1×2×3×…×n$.
2.1.1.2.2. Remarques
- $0!=1$ (produit vide)
- $1!=1$ ($1$ est à la fois $1$ et $n$)
- $n! = 1×2×3×…(n-1)×n$ (on fait apparaître l’avant-dernier terme).
- La factorielle est très importante en mathématique et apparait en dénombrement et lorsque l’on dérive plusieurs fois un polynôme.
2.1.1.2.3. Version impérative
def fact(n):
resultat = 1
facteur = 1
while facteur <= n:
resultat = resultat * facteur
facteur = facteur + 1
return resultat
print(fact(4))
Tableau de l’état des variables
| facteur | résultat |
|---|---|
| 1 | 1 |
| 2 | 1 puis 2 |
| 3 | 2 puis 6 |
| 4 | 6 puis 24 |
Remarque :
On aurait très bien pu commencer par $n$ au lieu de $1$, ce qui nous rapproche de la version suivante.
def fact(n):
resultat = n
facteur = n - 1
while facteur > 0:
resultat = resultat * facteur
facteur = facteur - 1
return resultat
print(fact(4))
2.1.1.2.4. Version récursive
L’algorithme est basé sur le fait que :
$$\begin{aligned} n! &= 1×2×3×…×(n-1)×n \\\\ &= n×(n-1)×…×3×2×1 \\\\ &= n × \underbrace{(n-1)×…×2×1}_{(n-1)!} \\\\ 4! &= 4 × \underbrace{3×2×1}_{3!} \\\\ \end{aligned}$$
def fact(n):
if n == 1: # comme 0! = 1, on peut aussi tester n == 0
return 1
else:
return n * fact(n-1)
print(fact(4))
On remarque que l’ordre d’entrée dans les fonctions se fait suivant les n
décroissants, mais que l’ordre de sortie se fait suivant les n croissants.
En déroulant l’algorithme à un certain rythme, on voit que la fin du else
n’est exécutée qu’après avoir atteint le point d’appui, et ceci dans chaque
appel.
En fait on pourrait constater la mise en abyme en suivant l’exécution de la fonction en réécrivant son code au lieu de l’appeler :
if 4 == 1:
resultat4 = 1
else:
resultat4 = 4 * fact(4-1)
# mais pour calculer fact(3),
if 3 == 1:
resultat3 = 1
else:
resultat3 = 3 * fact(3-1)
# mais pour calculer fact(2),
if 2 == 1:
resultat2 = 1
else:
resultat2 = 2 * fact(2-1)
# mais pour calculer fact(1),
if 1 == 1:
resultat1 = 1 # point d'appui
else:
# le point d'appui empeche d'aller plus loin
fact(1) = resultat1 = 1
fact(2) = resultat2 = 2 * fact(1) = 2 * 1
fact(3) = resultat3 = 3 * fact(2) = 3 * (2 * 1)
fact(4) = resultat4 = 4 * fact(3) = 4 * (3 * (2 * 1)) = 4 * 3 * 2 * 1
On en utilisant une syntaxe Python moderne :
>>> def fact(n): return 1 if n==1 else n*fact(n-1)
...
>>> fact(4)
24
>>> def fact(n): return 1 if n==1 else n*(1 if (n-1)==1 else (n-1)*fact(n-2))
...
>>> fact(4)
24
>>> def fact(n): return 1 if n==1 else n*(1 if (n-1)==1 else (n-1)*(1 if (n-2)==1 else (n-2)*fact(n-3)))
...
>>> fact(4)
24
2.1.1.2.4.1. Graphe des appels
fact(4)
| ^
1 | | 6
v |
fact(3)
| ^
2 | | 5
v |
fact(2)
| ^
3 | | 4
v |
fact(1)Chaque barre correspond à un appel (vers le bas) et à un retour (vers le haut).
Le retour ne se fait que lorsque le calcul appelé est terminé, notamment
lorsque ce calcul a eu ses retours. Par exemple fact(3) retourne si fact(2)
a retourné son résultat, qui à son tour retourne si fact(1) a retourné son
résultat.
2.1.1.2.4.2. Empilement des contextes
f(1)=1
f(2)=2×f(1) f(2)=2×f(1) f(2)=2×1
f(3)=3×f(2) f(3)=3×f(2) f(3)=3×f(2) f(3)=3×f(2) f(3)=3×2×1
f(4)=4×f(3) f(4)=4×f(3) f(4)=4×f(3) f(4)=4×f(3) f(4)=4×f(3) f(4)=4×f(3) f(4)=4×3×2×1
2.1.1.2.4.3. Suite d’égalités
$$\begin{aligned} 4! &= 4×3! \\\\ &= 4×(3×2!) \\\\ &= 4×(3×(2×1!)) \\\\ &= 4×(3×(2×1)) \\\\ &= 4×(3×2) \\\\ &= 4×6 \\\\ &= 24 \\\\ \end{aligned}$$
Cette suite d’égalités correspond au graphe des appels.
2.1.1.3. Somme de deux entiers positifs
La somme va être effectuée en se restreignant à des incrémentations et des décrémentations d’une unité.
2.1.1.3.1. Version impérative
def somme(m, n):
resultat = m
nbre_inc = n
while nbre_inc > 0:
resultat = resultat + 1
nbre_inc = nbre_inc - 1
return resultat
print(somme(2, 3))
Tableau de l’état des variables
| nbre_inc | résultat |
|---|---|
| 3 | 2 puis 3 |
| 2 | 3 puis 4 |
| 1 | 4 puis 5 |
2.1.1.3.2. Version récursive
L’algorithme est basé sur le fait que $m + n = (m+1) + (n-1)$ (c’est l’« invariant de boucle »). La fonction a deux paramètres et le point d’appui ne concerne que l’un des deux paramètres.
def somme(m, n):
if n == 0:
return m
else:
return somme(m+1, n-1)
print(somme(2, 3))
La différence fondamentale avec l’algorithme récursif de la factorielle est
qu’aucun travail n’est demandé entre l’appel récursif et le return. C’est
ce que l’on appelle en anglais un tail call (appel en queue). Une telle
fonction sera dite « à récursivité
terminale ». Cela
permet à certains compilateurs d’optimiser le code généré en termes
d’occupation de la mémoire.
On reconnaît la récursivité terminale au fait que le point d'appui est affiché en dernier. L'exécution n'est pas faite en V.
2.1.1.3.2.1. Graphe des appels
somme(2, 3)
|
somme(3, 2)
|
somme(4, 1)
|
somme(5, 0)
Le tail call permet une remontée quasi-directe dans le graphe, puisque
les return s'enchaînent directement.
2.1.1.3.2.2. Empilement des contextes
s(5,0)=5
s(4,1)=s(5,0) s(4,1)=s(5,0) s(4,1)=5
s(3,2)=s(4,1) s(3,2)=s(4,1) s(3,2)=s(4,1) s(3,2)=s(4,1) s(3,2)=5
s(2,3)=s(3,2) s(2,3)=s(3,2) s(2,3)=s(3,2) s(2,3)=s(3,2) s(2,3)=s(3,2) s(2,3)=s(3,2) s(2,3)=5
2.1.1.3.2.3. Suite d’égalités
$$\begin{aligned} 2+3 &= 3+2 \\\\ &= 4+1 \\\\ &= 5+0 \\\\ &= 5 \\\\ \end{aligned}$$
Cette suite d’égalités correspond aussi au graphe des appels.
2.1.1.4. Suite de Fibonacci
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …
--------|---|---|---|---|---|---|---|---
fibo(n) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | …
\___/ ^
+ ___/
On peut définir cette suite par :
$$ \left \{ \begin{array}{cl} u_0 = 0 \\\\ u_1 = 1 \\\\ \forall n \ge 0, u_{n+2} = … \\\\ \end{array} \right. $$
La dernière ligne peut aussi s’écrire $\forall n \ge 2, u_{n} = …$.
Remarque : Cette suite est très présente, tant dans la nature que dans la culture. Petite note historique : un siècle avant Fibonacci, Hemachandra faisait allusion à cette suite.
2.1.1.4.1. Version impérative
Laissée en exercice.
2.1.1.4.2. Version récursive
def fibo(n):
if ...:
return ...
else:
return ...
La différence avec la factorielle et la somme des entiers est cette fois que la fonction récursive s’appelle deux fois pour calculer une valeur.
2.1.1.4.2.1. Graphe des appels
Laissé en exercice.
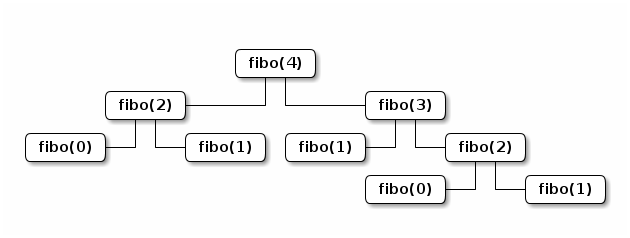
C’est un arbre et il est parcouru d’abord en profondeur.
On s’aperçois que si on ne s’organise pas mieux, on appelle par exemple
plusieurs fois fibo(2), et on gâche des calculs. C’est bien sûr de pire en
pire quand n augmente.
2.1.1.4.2.2. Suite d’égalités
$$\begin{aligned} F(4) &= F(2) + F(3) \\\\ &= (F(0) + F(1)) + (F(1) + F(2)) \\\\ &= (F(0) + F(1)) + (F(1) + (F(0) + F(1))) \\\\ &= (1 + 1) + (1 + (1 + 1)) \\\\ \end{aligned}$$
Cette suite d’égalités correspond aussi au graphe des appels : les parenthèses regroupent les termes des additions autant que les appels sont groupés par deux sous leur parent.
2.1.2. Comparaison des versions
2.1.2.1. Généralités
Même si le concept est difficile à saisir au début, un algorithme récursif est souvent plus concis, plus lisible, et surtout correspond souvent plus à la description de ce que l’on manipule plutôt qu’à la description de ce qui va finalement se passer. L’algorithme récursif découlera naturellement de la description du problème à résoudre.
2.1.2.2. Cas du jeu de Hanoï
Voir cette page pour une implémentation récursive. Il n’y a pas vraiment de concurrent non récursif.
2.1.3. Schéma général d’un algorithme récursif
Dans un algorithme récursif A, on distingue essentiellement deux parties :
- celle qui correspond au point d’appui,
- celle qui contient au moins un appel à
A.
On peut donc représenter A sous la forme :
Procedure A(p1,...,pn)
| Si cond alors
| | I1
| Sinon
| | I2
| | A(f(p1,...,pn))
| | I3
| | ...
| | A(g(p1,...,pn))
| | Im
p1, …, pn désignent les paramètres.
A(f(p1, …, pn)) = A(f1(p1, …, pn), …, fn(p1, …, pn)) où fi(p1,..., pn) est
une transformation du paramètre d’entrée pi (permet la récursion). De même
pour g.
Les fi(p1, …, pn) doivent faire évoluer le paramètre pi vers le point
d’appui, afin que l’algorithme se termine.
I1, I2, …, Im représentent chacune une suite d’instructions (éventuellement
vide) qui ne comporte aucun appel à A.
La condition cond permet de distinguer le traitement du point d’appui du
traitement courant est une expression booléenne contenant au moins un pk
parmi les paramètres p1, …, pn.
2.1.4. Schéma général d’une fonction récursive à une variable
Fonction FR(x)
| Si «x est un point d’appui» alors
| | Retourner f(x) # Pas d’appel à FR ici !
| Sinon
| | Retourner g(FR(h(x)), x) # h rapproche x du point d’appui.
Dans les cas simples, g n’appelle FR qu’une fois.
h doit donner des images de plus en plus proches du point d’appui afin que
l’algorithme se termine.
2.1.5. Un peu de culture
Certains langages n’autorisent pas les appels récursifs.
À l’opposé, certains langages, comme par exemple les langages fonctionnels, ne se servent que de la récursivité pour faire l’équivalent des boucles des autres langages.
Python permet la récursivité, mais n’optimise pas les appels terminaux. Il est donc possible d’atteindre la limite arbitraire fixée à 1000 appels. Pour plus de détails, voir la section RuntimeError: maximum recursion depth exceeded du mémento Python.
2.2. Structures de données
Les listes et les arbres peuvent être vus comme des structures de données récursives (voir l’article sur Wikipedia).
2.2.1. Listes
2.2.1.1. Définition récursive
Une liste est :
- soit vide,
- soit elle peut être vue comme un premier élément suivi d’une… liste.
2.2.1.2. Travail récursif sur les listes
En utilisant une fonction binaire (acceptant deux arguments), on peut implémenter une fonction acceptant une liste qui lui correspond. Par exemple, on peut additionner les éléments d’une liste en ajoutant un élément au résultat accumulé. Nous l’avons déjà fait en version impérative, c’est le moment de faire la version récursive.
Rappel : vous aurez besoin de savoir manipuler listes en Python.
>>> liste = [1, 3, 5, 7]
>>> liste[0]
1
>>> liste[1 : len(liste)] # on peut omettre len(liste)
[3, 5, 7]
>>> liste[1:]
[3, 5, 7]
Exemple avec la fonction somme définie récursivement à l’aide de + :
def somme(liste):
if len(liste) == 0:
return 0
else:
# liste[0] est le premier element de liste
# liste[1:] est liste privee de son premier element
return liste[0] + somme(liste[1:])
Note 1 : le point d’appui ne sert pas qu’à protéger du cas où la liste est vide, ce cas sera forcément atteint.
Note 2 : il est possible d’utiliser le test len(liste) == 1, c’est
ce que l’on a envie de faire lorsque l’on essaie l’algorithme à la main. À vous
d’imaginer comment adapter le reste.
À vous de tester cet algorithme avec [2, 7].
2.2.2. Chaînes de caractères
Les algorithmes récursifs peuvent aussi très bien s’appliquer à des problèmes concernant les chaînes de caractères, puisqu’assez similaires à des listes.
Nous étudions ici un exemple détourné de chaîne de caractères où chaque caractère est un chiffre. À quoi peut servir Ce fichier ?
Notons que la fonction principale n’est pas récursive, mais qu’elle fait appel à une fonction une auxiliaire récursive, qui elle admet un accumulateur dans sa signature.
2.2.3. Arbres binaires
Un arbre binaire est :
- soit une feuille,
- soit un assemblage de… deux arbres.
Les arbres en général (structure d’un système de fichiers, entre autres), mais aussi les arbres binaires (organisation de calculs, de données, tris, entre autres) sont d’une importance capitale en informatique.
