Graphes orientés
1. Activité introductive
1.1. Énoncé
Voir feuille (non numérisée).
1.2. Réponses
On ne cherche à coder que les destinations possibles à partir de chaque carrefour. On n’attache aucune importance à :
- la position des nœuds, leur forme…
- la taille des flèches, leur forme…
La seule chose qui va nous aider pour la suite, c’est de mettre deux flèches plutôt qu’une à double pointe.
Attention, même si on considère qu'étant à un carrefour on peut y aller (puisqu'on y est), on ne met de flèche que s'il y a une rue.
1.3. Un peu de culture
- Jeux de désenchevêtrement
Lorsque l’on joue à ces jeux, les points et les segments bougent, mais le graphe correspondant reste inchangé.
Mais a-t-on ici des graphes simples orientés ?
2. Modes de représentation
2.1. Flèches
C’est le schéma réalisé lors de l’activité, avec les flèches.
On préfèrera deux simples flèches au lieu d’une double, plus pratique pour compter le nombre de flèches.
2.2. Notation ensembliste
2.2.1. Définition d’un graphe simple orienté
Un graphe simple orienté est défini par deux ensembles $X$ et $U$.
$X = \left\{x_1, x_2, x_3,… x_n\right\}$ est un ensemble fini qui contient les sommets ou les nœuds du graphe.
$U = \left\{ (x_i, x_j),… \right\}$ est un ensemble de couples de sommets, appelés arcs (ou arêtes orientées), qui décrit les relations entre les nœuds.
Remarque :
Les couples mathématiques sont ordonnés et peuvent contenir deux fois le même
objet.
2.2.2. Exemple
À partir de l’activité :
$X = \left\{ A, B, C, D \right\}$
$U = \left\{ (A, B) ; (A, C) ; (A, D) ; (B, C) ; (C, B) ; (C, D) ; (D, A) ; (D, D) \right\}$
2.2.3. Définition des successeurs et des prédécesseurs
On dit que $x_j$ est un successeur de $x_i$ si $(x_i, x_j) \in U$, autrement dit si $(x_i, x_j)$ est un arc du graphe. On note $\Gamma (x)$ l’ensemble des successeurs de $x$.
On dit que $x_i$ est un prédécesseur de $x_j$ si $(x_i, x_j) \in U$, autrement dit si $(x_i, x_j)$ est un arc du graphe. On note $\Gamma^{-1} (x)$ l’ensemble des prédécesseurs de $x$.
2.2.4. Exemples
À partir de l’activité :
- successeurs :
- $\Gamma (A) = \left\{B,C,D\right\}$
- $\Gamma (B) = \left\{C\right\}$
- $\Gamma (C) = \left\{B,D\right\}$
- $\Gamma (D) = \left\{A,D\right\}$
- prédécesseur :
- $\Gamma ^ {-1} (A) = \left\{D\right\}$
- $\Gamma ^ {-1} (B) = \left\{A,C\right\}$
- $\Gamma ^ {-1} (C) = \left\{A,B\right\}$
- $\Gamma ^ {-1} (D) = \left\{A,C,D\right\}$
On organise souvent ces informations dans des tableaux:
| x | successeurs de x | | x | prédécesseurs de x |
+-----+-------------------+ +-----+---------------------+
| | | | | |
Remarque : Un seul de ces tableau suffit pour connaître entièrement le graphe, et par exemple construire l'autre tableau.
2.3. Matrice
2.3.1. Définition
La matrice d’adjacence d’un graphe simple orienté à $n$ sommets est la matrice carrée $n×n$ où, si l’on note $a_{ij}$ son terme général :
- $a_{ij} = 1$ si $(x_i, x_j)$ est un arc du graphe,
- $a_{ij} = 0$ sinon.
2.3.2. Exemple
À partir de l’activité :
$$M = \begin{pmatrix} 0 & 1 & 1 & 1 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 1 & 0 & 0 & 1 \\\\ \end{pmatrix}$$
2.3.3. Remarques
- Cette matrice est dite « d’adjacence » car code l’information des sommets qui sont dits « adjacents ».
- Il y a autant de 1 que d’arcs.
- On trouve les successeurs en lisant vers la droite, les prédécesseurs en
lisant vers le bas. Autrement dit :
- les successeurs du premier nœud sont dans la première ligne, ceux du deuxième dans la deuxième…
- les prédécesseurs du premier nœud sont dans la première colonne, ceux du deuxième dans la deuxième…
- Cette matrice sera parfois considérée à coefficients entiers (1+1=2), parfois à coefficients booléens (1+1=1).
3. Chemins
3.1. Définitions
Dans un graphe simple orienté, on dira que :
- un chemin est une liste finie et ordonnée de sommets dont chacun des sommets (sauf le dernier) a le sommet suivant comme successeur.
- un circuit est un chemin dont le premier et le dernier sommet sont identiques.
- Un chemin hamiltonien est un chemin qui passe une fois et une seule par chaque sommet du graphe.
- Une boucle est une arête qui joint un sommet à lui-même.
3.2. Exemples
À partir de l’activité :
- $(D, A, C)$, $(D, A, D, A, D, A)$, $(A, B)$, $(D, D, D, D, D)$ sont des chemins.
- $(A, B, C, D, A)$, $(D, A, C, D)$, $(A, D, A, D, A)$, $(D, D)$ sont des circuits.
- $(A, B, C, D)$ et $(D, A, C, B)$ sont des chemins hamiltoniens.
3.3. Longueur d’un chemin
3.3.1. Définition
La longueur d’un chemin à $p$ sommets (possiblement identiques) vaut $p-1$.
Autrement dit, c’est le nombre d’arcs qui le composent.
3.3.2. Propriété
3.3.2.1. Énoncé
Soit $M$ la matrice d’adjacence d’un graphe simple orienté à $n$ sommets.
Le nombre de chemins de longueur $p$ (donc à $p+1$ sommets) allant de $x_i$ à $x_j$ est le coefficient de $M^p$ se trouvant à la ligne $i$ et à la colonne $j$.
Attention, ici $M$ est considérée à coefficients entiers.
3.3.2.2. Exemples
À partir de l’activité étudions les chemins de longueur 1, puis 2, puis 3…
3.3.2.2.1. Chemins de longueur 1
D’une part, $M^1 = M$.
D’autre part, les chemins de longueur 1 sont les arcs du graphe. On retrouve bien la définition de $M$ : présence (1) ou non (0) d’un arc.
3.3.2.2.2. Chemins de longueur 2
En calculant le coefficient ligne 1 colonne 2 de $M^2$, on s’aperçoit que l’on cumule le nombre de chemins partant de A et allant vers B et passant par un seul point intermédiaire :
- $A \overset{a_{11}}{\longrightarrow} A \overset{a_{12}}{\longrightarrow} B$
- $A \overset{a_{12}}{\longrightarrow} B \overset{a_{22}}{\longrightarrow} B$
- $A \overset{a_{13}}{\longrightarrow} C \overset{a_{32}}{\longrightarrow} B$
- $A \overset{a_{14}}{\longrightarrow} D \overset{a_{42}}{\longrightarrow} B$
Par exemple, $a_{32}$ est le nombre d’arcs (0 ou 1) allant de C à B.
Le produit matriciel est donc l’outil naturel pour ce calcul.
3.3.2.2.3. Chemins de longueur 3
Un chemin de longueur 3 peut être considéré comme un chemin de longueur 2 auquel on a ajouté un arc. Si on considère les chemins de longueur 3 allant de A à D, il suffit de :
- partir de A (donc regarder sa ligne),
- choisir un des points intermédiaires possibles : A, B, C ou D,
- comptabiliser les chemins de longueur 2 partant de A allant au point choisi,
- ajouter un arc arrivant à D, si possible : si oui, on multiplie par 1, sinon on multiplie par 0.
- Enfin, on ajoute toutes ces possibilités.
Ici on note $b_{ij}$ les coefficients de $M^2$.
- $A \overset{b_{11}=1}{\longrightarrow} A \overset{a_{12}=1}{\longrightarrow} D$
- $A \overset{b_{12}=1}{\longrightarrow} B \overset{a_{22}=0}{\longrightarrow} D$
- $A \overset{b_{13}=1}{\longrightarrow} C \overset{a_{32}=1}{\longrightarrow} D$
- $A \overset{b_{14}=2}{\longrightarrow} D \overset{a_{42}=1}{\longrightarrow} D$
On s’aperçoit que l’on calcule le coefficient à la 1ère ligne et 4ème colonne de la matrice $M^2 × M = M^3$.
On remarque aussi que l’on peut considérer $M^3 = M × M^2$.
3.3.2.2.4. Chemins de longueur 4
Idem avec $M^4 = M × M^3 = M^2 × M^2 = M^3 × M$.
4. Fermeture transitive d’un graphe et matrice d’accessibilité
4.1. Définition
La fermeture transitive d’un graphe $G$ est notée $\hat G$ (prononcé « gé chapeau » et est le graphe obtenu en :
- conservant les nœuds et les arcs de $G$,
- ajoutant si nécessaire les arcs $(x,y)$ s’il existe un chemin de $x$ à $y$.
4.2. Remarques
- « Les amis de mes amis sont mes amis. »
- $\hat G$ nous dit si un nœud est accessible depuis un autre dans $G$.
- On peut arriver à un graphe complet (tous les arcs possibles).
4.3. Exemples
- Donner la fermeture de l’exemples du début du cours.
- Soit $G$ le graphe comportant les nœuds $\left\{x_1, x_2, x_3, x_4\right\}$
et trois arcs : $\left\{(x_1, x_2), (x_2, x_3), (x_3, x_4)\right\}$.
Donner la fermeture de ce graphe en utilisant le code couleur :- vert pour les arcs issus d’un chemin de longueur 2 dans $G$,
- rouge pour les arcs issus d’un chemin de longueur 3 dans $G$,
- bleu pour les arcs issus d’un chemin de longueur 4 dans $G$.
4.4. Calcul
Si $M$ est la matrice d’adjacence de $G$, on note $\hat M$ la matrice d’adjacence de $\hat G$, appelée la matrice d’accessibilité de $G$. On a :
$$\hat M = M \oplus M^{\left[2\right]} \oplus M^{\left[3\right]} \oplus ... \oplus M^{\left[n\right]}$$
où $\oplus$ et $\left[i\right]$ sont la somme booléenne et la puissance booléenne des matrices, et $n$ la taille du graphe $G$.
4.5. Calcul avec le deuxième exemple
Calculer $M^{\left[2\right]}$, $M^{\left[3\right]}$ et $M^{\left[4\right]}$, puis les additionner avec la somme booléenne.
Remarque : Pas besoin de calculer $M^5$ car elle ne peut pas ajouter un nouvel arc. En effet, il n’y a que quatre nœuds.
5. Ordonnancement et planification
5.1. Unités
5.1.1. Énergie et puissance
En physique, l’énergie est, entre autres, ce que produit ou reçois un système suite à un travail.
L’énergie se mesure en joules (ou parfois calories).
La puissance est la quantité d’énergie par unité de temps. Elle se mesure en Watts (joules par seconde).
On comprend ainsi que le Wh qui est sur nos factures (qui se dit « watt heure ») est une autre unité pour l’énergie, qui vaut 3600 joules. C’est l’énergie produite par une puissance de 1 W pendant une heure (on multiplie).
5.1.2. Dans l’industrie informatique
L’unité de la puissance de travail est l’homme (ce qui est assez sexiste).
L’unité de temps est le jour.
Le produit des deux est en quelque sorte une unité d’énergie : le jour-homme : le travail produit par une personne pendant un jour.
Exemple : la quantité 6jh peut représenter le travail effectué :
- par une personne pendant 6 jours,
- par 3 personnes pendant 2 jours,
- par 6 personnes pendant 1 jour,
- ...
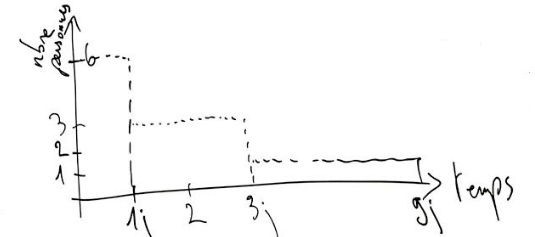
Ici, le travail réalisé est donné par la surface des rectangles.
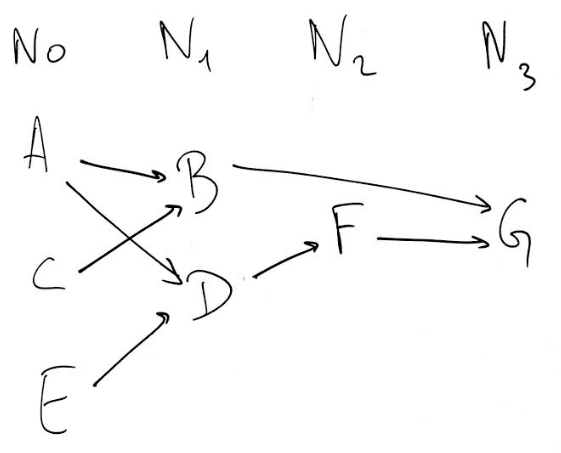
5.2. Niveaux d’un graphe
Pour un graphe ne comportant pas de cycle, on peut classer les nœuds par niveaux. Pour cela, on commence par construire le tableau des prédécesseurs (voir plus haut pour la définition).
| x | prédécesseurs de x |
+-----+---------------------+
| A | rien |
| B | C, A |
| C | rien |
| D | A, E |
| E | rien |
| F | D |
| G | B, F |
Le niveau zéro est constitué des nœuds qui n’ont pas de prédécesseur. Ici ce sont A, C et E.
Dans la colonne de droite, on barre ces nœuds.
Le niveau un est constitué des nœuds qui n’ont pas de prédécesseurs après avoir barré les nœuds de niveau zéro. Ce sont B et D.
Le niveau deux est constitué des nœuds qui n’ont pas de prédécesseurs après avoir barré les nœuds de niveau zéro et un. C’est ici F.
Idem pour le niveau trois, où on trouve le dernier nœud G.
L’organisation « par niveaux » permet de dessiner le graphe avec des flèches qui vont toutes vers la droite.
5.3. Graphes pondérés, ou valués
5.3.1. Définition
C’est un graphe où on associe à chaque arc un nombre : son poids ou sa valeur.
5.3.2. Valeur d’un chemin
La valeur d’un chemin est la somme des valeurs des arcs qui le composent.
Abus de langage : on dit parfois « longueur » à la place de « valeur ».
5.3.3. Exemple de graphes pondérés
- Carrefours avec durées de déplacement
- Chemins dans une jungle avec des cartons de nourriture
- Tâches à réaliser, dépendantes les unes des autres, avec un certain temps nécessaire pour leur réalisation
- …
5.3.4. Exemples de problèmes
- Trouver le chemin de valeur maximale.
- Trouver le chemin de valeur minimale.
5.4. Méthode MPM
Nous allons ici présenter la méthode MPM (Méthode des potentiels métra). Il est possible d’obtenir les mêmes résultats avec la méthode PERT (de l’anglais « program evaluation and review technic »). Voir sur Wikipedia MPM et PERT.
5.4.1. Mise en place
- Modéliser le projet par un graphe : les tâches sont des nœuds, les dépendances sont des arcs, dont la valeur est la durée de la tâche d’origine de l’arc.
- Organiser le graphe par niveaux, indiquer les durées sur les arcs.
- Parcourir le graphe de gauche à droite pour obtenir les dates
au plus tôt (comme si on « penchait » le graphe vers la gauche).
Max(Dates au plus tôt précédentes + durées précédentes correspondantes) - Parcourir le graphe de droite à gauche pour obtenir les dates
au plus tard (comme si on « penchait » le graphe vers la droite).
Min(Date au plus tard suivantes) - durée de la tâche
5.4.2. Marges
5.4.2.1. Marge totale
C’est le retard autorisé pour une tâche (à partir de la date au plus tôt) sans qu’elle ne retarde la fin du projet.
Date au plus tard - Date au plus tôt
5.4.2.2. Marge libre
C’est le retard autorisé pour une tâche (à partir de la date au plus tôt) sans retarder aucune des tâches suivantes.
Min(Dates au plus tôt suivantes) - (Date au plus tôt de la tâche + Durée de la tâche)
5.4.2.3. Marge absolue ou certaine
Rarement étudiée.
C’est le retard autorisé (à partir de la date au plus tard) sans retarder la fin du projet.
Min(Date au plus tôt suivantes) - (Date au plus tard tâche S + Durée tâche S)
5.4.3. Tâches critiques et chemin critique
Dans un projet, il existe toujours au moins un chemin qui :
- part d’une tâche au niveau zéro,
- arrive à la tâche du dernier niveau,
- et qui est constitué de tâches de marge totale nulle.
C’est le (ou les) chemin critique. Les tâches le constituant sont les tâches critiques.
6. Arbres
6.1. Présentation
Certains graphes sont dits arborescents.
- une racine (niveau 0)
- chaque nœud a :
- au plus un parent
- au moins un parent (sauf la racine)
Représentation préférée : par niveaux et du haut vers le bas, en commençant par la racine.
6.2. Exemples
- en généalogie (vocabulaire employé en informatique)
- en programmation orientée objet (dans certains langages seulement)
- …
6.3. Outils
Les outils vus précédemment sur les graphes s’appliquent aussi !
