1. Opérations sur les ensembles

$A$, $B$ et $C$ sont des parties (sous-ensembles) d’un ensemble $E$.

1.1. Simplifications élémentaires

Réduire les expressions à une expression d’un seul symbole à choisir parmi $\emptyset$, $E$ et $A$ :

1. $A \cup \emptyset$
2. $A \cap \emptyset$
3. $A \cup E$
4. $A \cap E$
5. $A \cup A$
6. $A \cap A$
7. $A \cap ((\emptyset \cup A) \cap E)$

1.2. Simplifications

Simplifier les expressions suivantes :

1. $A \cap (\overline A \cap B)$
2. $A \cup (\overline A \cup B)$
3. $A \cup (\overline A \cap B)$
4. $(\overline A \cap B) \cup (A \cap B)$

1.3. Visualisations

Représenter graphiquement :

1. $(\overline A \cap B) \cup (B \cap C)$
2. $A \cap \overline B \cap C$

1.4. Produits cartésiens

On a $E = \left\{5;6\right\}$ et $F = \left\{7;8;9\right\}$.

Pour chaque ensemble donné ci-après, le décrire et donner son cardinal :

$E×F$, $F×E$, $E² (=E×E)$, $F²$ et $E³$.

2. Relation donnée par son graphe

Dans cet exercice, on définit une relation $\mathcal R$ sur un ensemble $E$.

On note $E = \left\{ 1, 2, 3, 4 \right\}$ et $\Gamma = \left\{ (1;1); (1;2); (2;1); (2;2); (3;3); (3;4); (4;3); (4;4)\right\}$.

• Représenter la relation avec :
  • son diagramme sagittal,
  • sa matrice,
  • son tableau.
• $\mathcal R$ est-elle une relation d’équivalence ? d’ordre ?
• Si c’est une relation d’ordre, est-ce un ordre total ? partiel ?
• Peut-on ajouter une flèche pour rendre la relation non transitive ?

3. Autres relations

Pour chaque relation $\mathcal R$ :

• $\mathcal R$ est-elle une relation d’équivalence ? d’ordre ?
• Si c’est une relation d’ordre, est-ce un ordre total ? partiel ?

3.1. Sans couples

1. $E = \mathbb Z$ Soit $n$ un entier naturel non nul. $a \mathcal R b \Leftrightarrow a \equiv b \left[ n \right]$
2. $E = \mathbb N ^*$ $m \mathcal R n \Leftrightarrow n ~\text{est un multiple de}~m$
   Bonus : l’ensemble $\left\{ 4, 5, 6, 7, 8, 9, 10 \right\}$ possède-t-il un plus petit élément au sens de $\mathcal R$ ?
3. $E = \mathbb R$ $x \mathcal R y \Leftrightarrow x^2 - y^2 = x - y$
4. Soit $F$ un ensemble. On se fixe un ensemble $A$ dans $F$. $E = \mathcal P \left(F\right)$ c’est-à-dire les sous-ensembles de $F$. $X \mathcal R Y \Leftrightarrow A \cap X = A \cap Y$
   Pour y voir clair, on peut prendre un exemple comme :
   $F = \left\{ 1, 2, 3, 4 \right\}$ et $A = \left\{ 1, 2 \right\}$.

3.2. Les éléments sont des couples

1. $E = \mathbb R ^2$ $(a,b) \mathcal R (c,d) \Leftrightarrow a^2+b^2=c^2+d^2$
2. $E = \mathbb R ^2$ $(x,y) \mathcal R (x',y') \Leftrightarrow x \le x' \wedge y \le y'$
3. $E = \mathbb R ^2$ $(x,y) \mathcal R (x',y') \Leftrightarrow x < x' \vee y \le y'$

4. Applications

4.1. Injectivité et surjectivité

4.1.1. Propriétés avec le cardinal

On rappelle que le cardinal d’un ensemble $A$, noté $Card(A)$, est le nombre d’éléments qu’il contient.

1. Représenter schématiquement (avec des flèches) une application injective $f$ de $E$ dans $F$ avec $Card(E) = 4$ et $Card(F) = 3$.
2. Représenter schématiquement (avec des flèches) une application surjective $f$ de $E$ dans $F$ avec $Card(E) = 3$ et $Card(F) = 4$.

4.1.2. Lecture des propriétés

Les graphes donnés ci-dessous représentent-ils des applications ? des injections ? des surjections ? des bijections ? Justifier vos réponses.

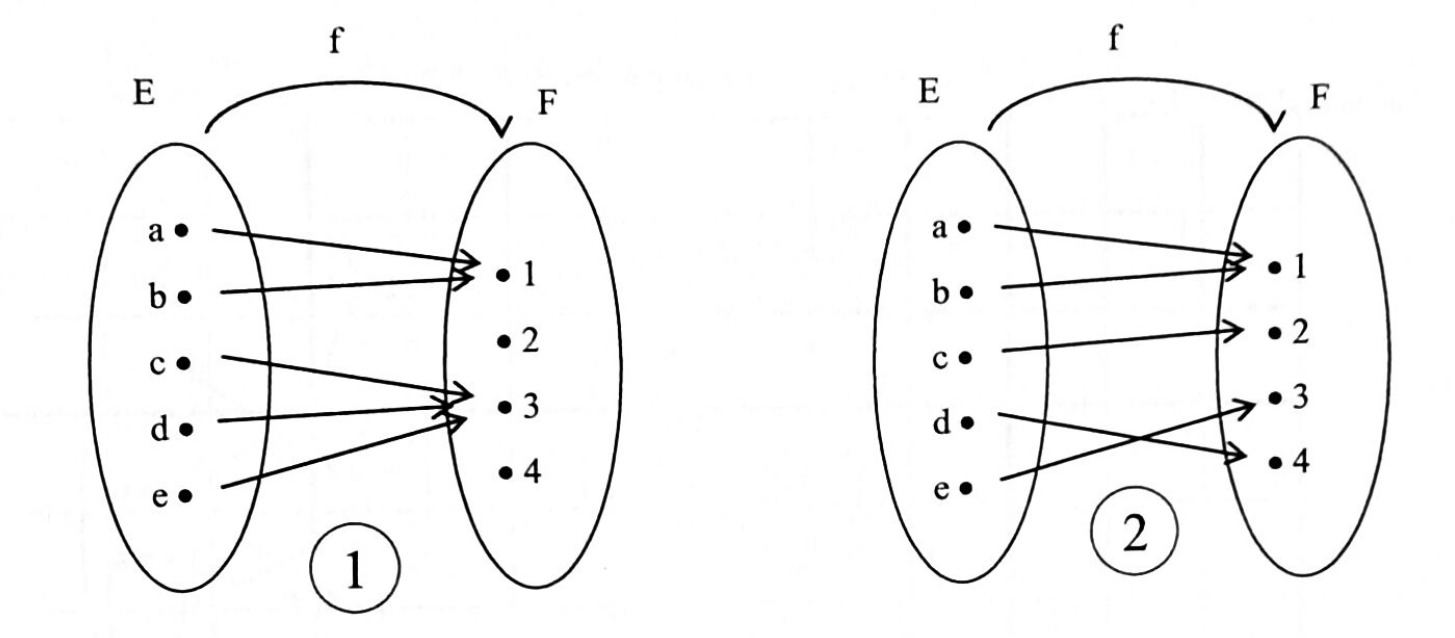
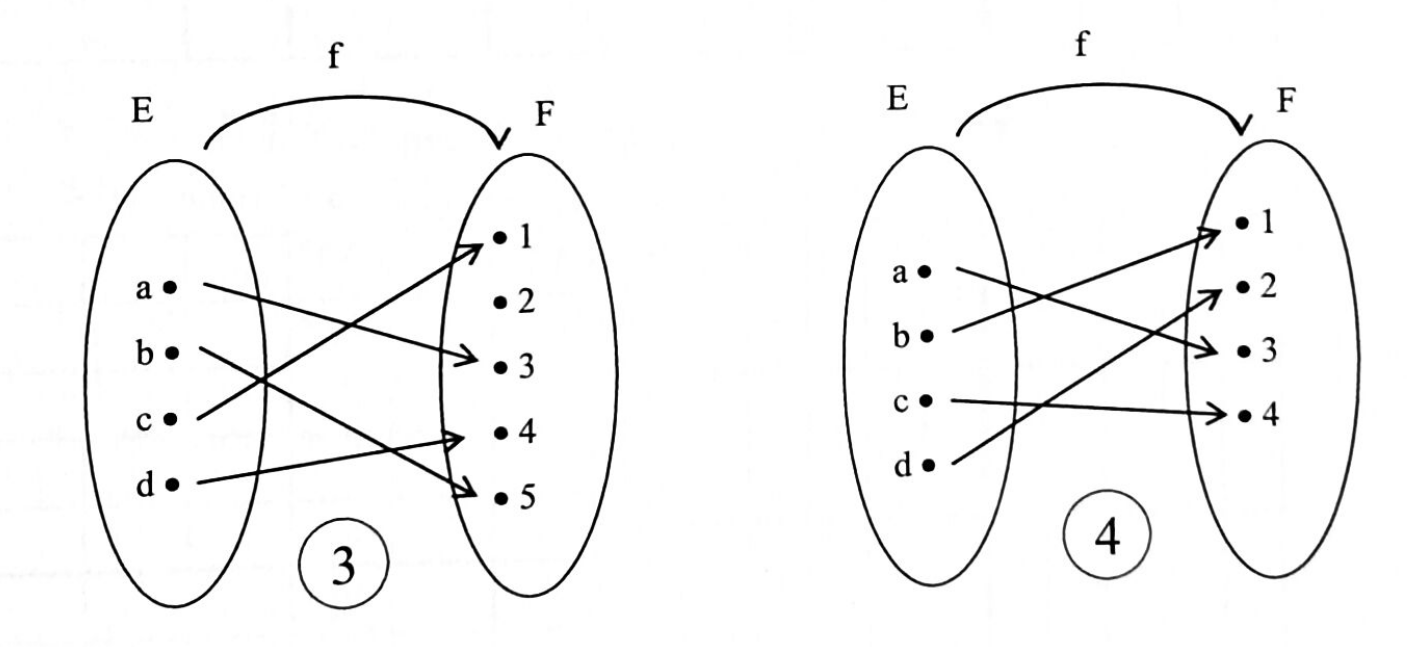
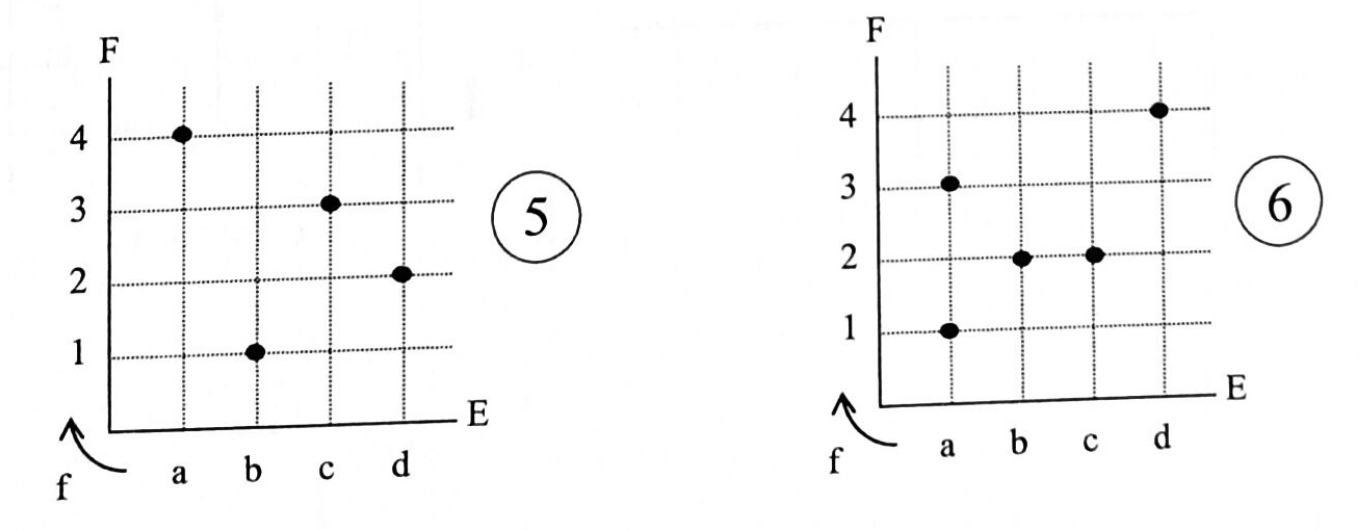
Les représentations graphiques données ci-dessous sont-elles des représentations d’applications définies de $\mathbb R$ dans $\mathbb R$ ? d’injections de $\mathbb R$ dans $\mathbb R$ ? de surjections de $\mathbb R$ dans $\mathbb R$ ? Justifier vos réponses.

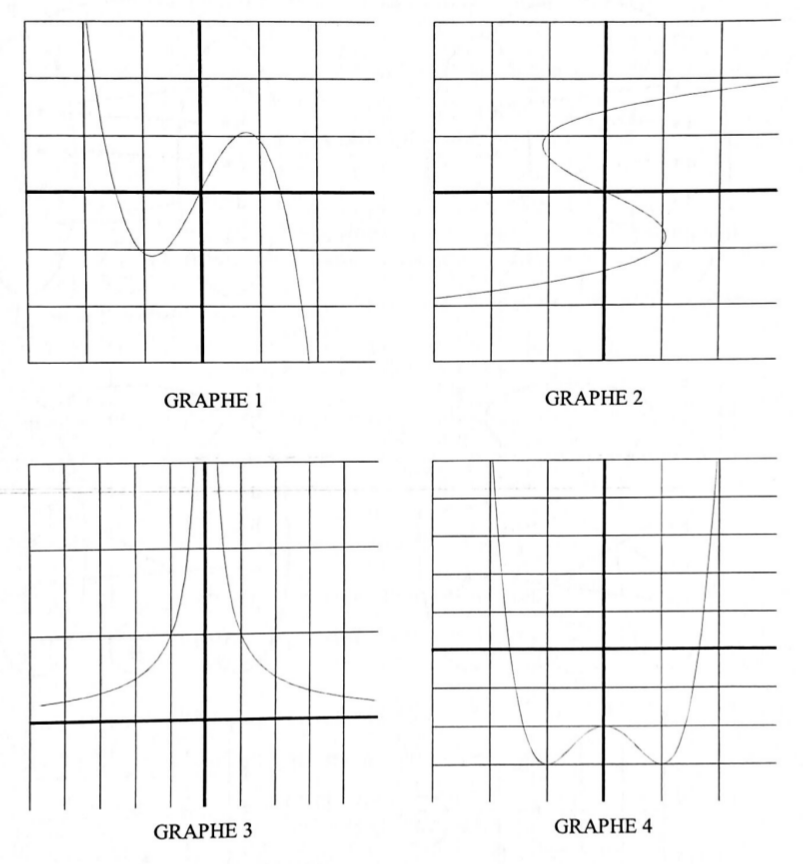
4.2. Composition

4.2.1. Premier exercice

Les applications $f$ et $g$, respectivement de $E$ dans $F$ et de $F$ dans $E$, sont définies par les diagrammes ci-dessous.

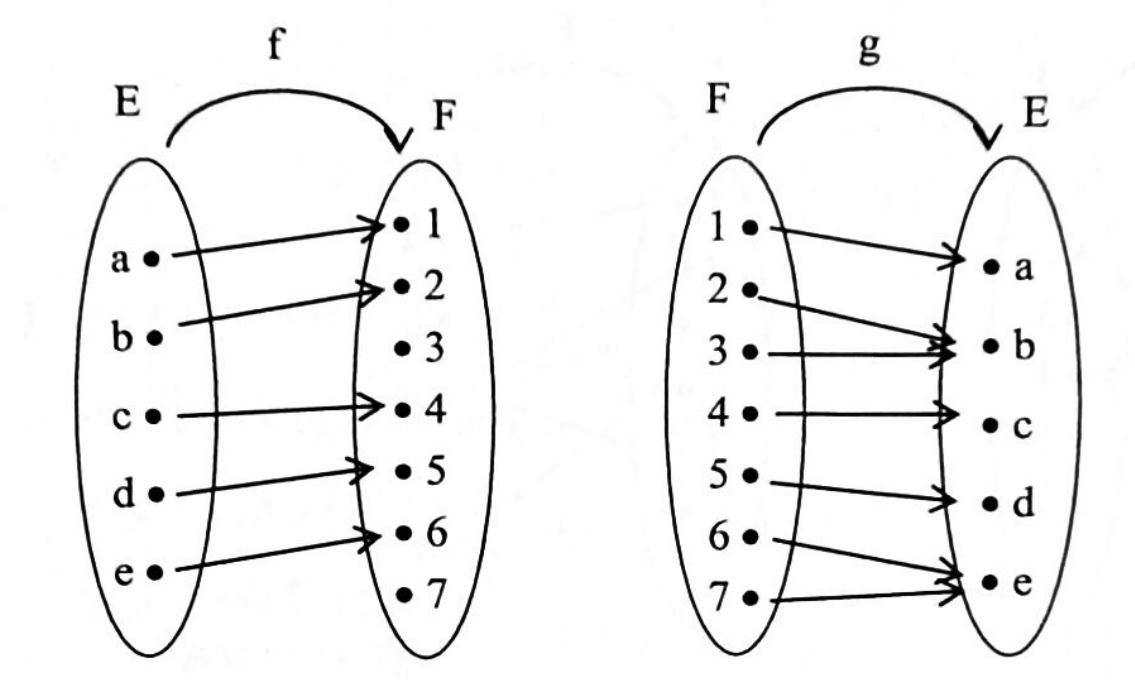
1. $f$ est-elle injective ? surjective ?
2. Mêmes questions pour $g$.
3. Déterminer l’application $g \circ f$. Est-elle injective ? surjective ?
4. Mêmes questions pour $f \circ g$.

4.2.2. Second exercice

Les applications $f$ et $g$, respectivement de $E$ dans $F$ et de $F$ dans $E$, sont définies par les diagrammes ci-dessous.

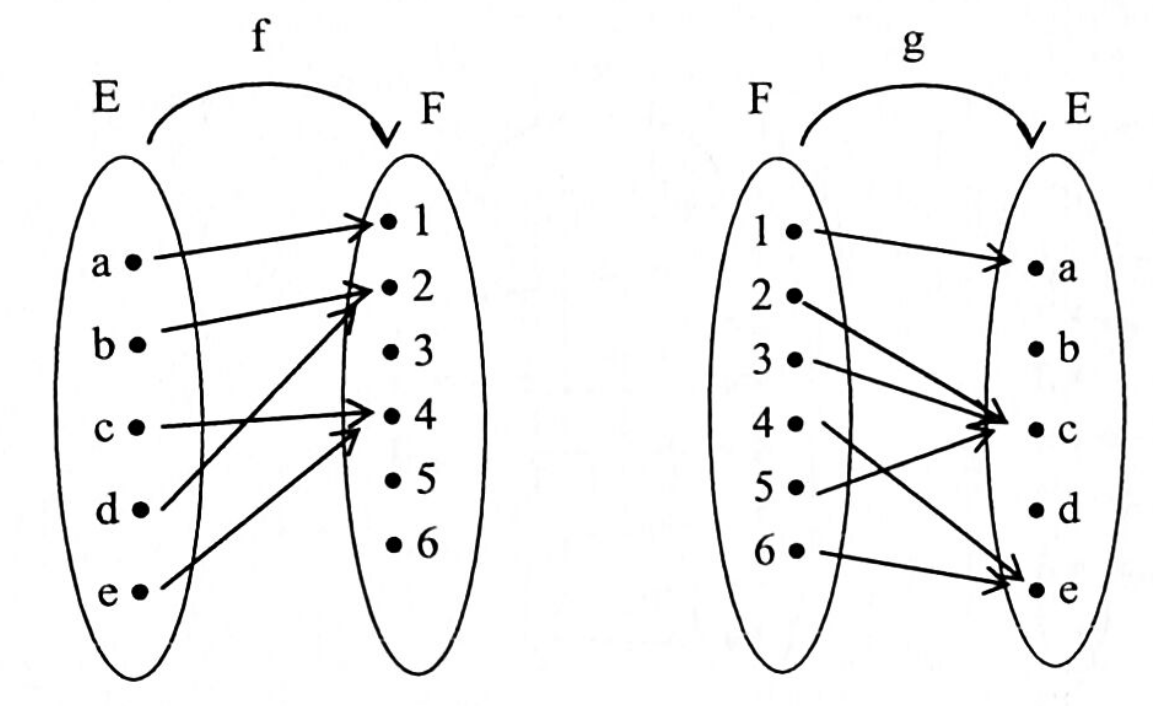
1. Déterminer l’application $g \circ f$.
2. Est-elle injective ?
3. Est-elle surjective ?

4.3. Image et image réciproque d’ensembles et composition

Les applications $f$ et $g$, respectivement de $E$ dans $F$ et de $F$ dans $G$, sont définies par les diagrammes ci-dessous.

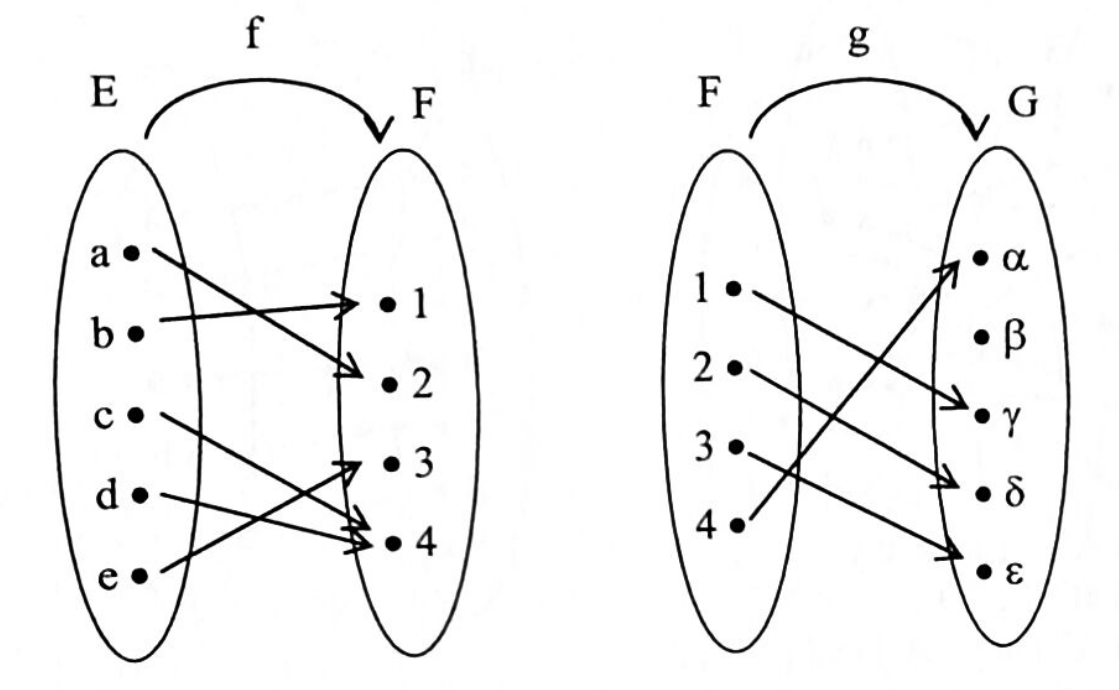
1. $f$ est-elle injective ? $g$ est-elle surjective ?
2. Déterminer les ensembles $f(\left\{a,c,e\right\})$ et $g(\left\{2; 4\right\})$.
3. Déterminer les ensembles $f^{-1}(\left\{2; 4\right\})$ et $g^{-1}(\left\{\alpha, \gamma\right\})$.
4. Représenter l’application $g \circ f$.

4.4. Calculs sur ensembles images et images réciproques

Soit $f$ l’application de $E$ dans $F$ définie par le graphe :

$$\Gamma = \left\{(a;1); (b;2); (c; 4); (d; 2); (e;4)\right\}$$

4.4.1. Injectivité et surjectivité

$f$ est-elle injective ? surjective ?

4.4.2. Intersection et union d’images

Soit $A=\left\{a, b, c\right\}$ et $A'=\left\{a, d, e\right\}$.

1. Déterminer $f(A)$ et $f(A')$.
2. Comparer $f(A\cap A')$ et $f(A)\cap f(A')$.
3. Comparer $f(A\cup A')$ et $f(A)\cup f(A')$.

4.4.3. Intersection et union d’images réciproques

Soit $B=\left\{1,2\right\}$ et $B'=\left\{3,4\right\}$.

1. Déterminer $f^{-1}(B)$ et $f^{-1}(B')$.
2. Comparer $f^{-1}(B\cap B')$ et $f^{-1}(B)\cap f^{-1}(B')$.
3. Comparer $f^{-1}(B\cup B')$ et $f^{-1}(B)\cup f^{-1}(B')$.