1. Rappels

1.1. Nombre dérivé et tangente à une courbe

1.1.1. Définition

Soit $I$ un intervalle contenant un nombre réel $a$ et $f$ une fonction définie sur $I$. On dit que la fonction $f$ est dérivable en $a$ si la limite du rapport $\frac{f(a+h)-f(a)}{h}$ lorsque $h$ tend vers 0, existe et est égale à un nombre réel $l$.

Ce nombre $l$ est appelé nombre dérivé de la fonction $f$ en $a$.

1.1.1.1. Remarques

1. On peut écrire une définition similaire avec $h=x-x_0$.
2. racine (et sinus cardinal ?) ne sont pas dérivables en 0.
3. $l$ sera bientôt écrit $f'(a)$.

1.1.2. Définition

Soit $f$ une fonction définie sur un intervalle $I$, dérivable en $a$, nombre réel appartenant à $I$, et de nombre dérivé $l$ en $a$.

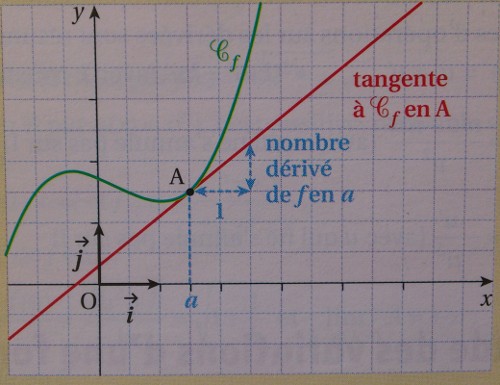
Soit $C_f$ la courbe représentative de la fonction $f$ dans un repère $(O, \vec i, \vec j)$ du plan et $A$ le point de $C_f$ d'abscisse $a$.

La tangente à la courbe $C_f$ au point $A$ est la droite qui passe par $A$ et qui a comme coefficient directeur le nombre dérivé $l$.

2. Dérivées de fonctions composées

2.1. Fonction affine, puis quelconque

$f(x) = w(ax + b)$