Modif a1aac2b1

Date:   Fri Oct 10 22:04:41 2014 +0200

    TS lim de fctions: qques modifs suite à la séance.

diff --git a/input/TS-02-Limites_de_fonctions.md b/input/TS-02-Limites_de_fonctions.md
index 0d3a3ed..040754c 100644
--- a/input/TS-02-Limites_de_fonctions.md
+++ b/input/TS-02-Limites_de_fonctions.md
@@ -242,8 +242,12 @@ On pourra écrire aussi, respectivement :
 * $\lim\limits_{x \to x_0^-} f(x)$ ou
 * $\lim\limits_{x \to x_0^+} f(x)$.

-On parlera respectivement de « limite à gauche de $x_0$ » et de
-« limite à droite de $x_0$ ».
+**Remarques** :
+
+* On parlera respectivement de « limite à gauche de $x_0$ » et de
+  « limite à droite de $x_0$ ».
+* Le petit signe + ou - n’a aucun rapport avec le signe de $x_0$, sauf bien
+  sûr si $x_0 = 0$.

 **Exemple** : Donner les limites autour de 0 de la fonction *inverse*.

@@ -258,11 +262,11 @@ r"""$\lim\limits_{x \to 0^-} \frac{1}{x} = -\infty$ et
 Comparaison de f avec sa limite
 -------------------------------

-Lorsque $f$ a une limite finie $l$ à l'inf en $\alpha$ ($-\infty$ ou $+\infty$) et que,
-au voisinage de $\alpha$, les images par $f$ sont inférieures, ou
-respectivement supérieure à la limite $l$, on écrira :
+Lorsque $f$ a une limite finie $l$ en $\alpha$ où $\alpha = -\infty$ ou
+$\alpha = +\infty$ et que, au voisinage de $\alpha$, les images par $f$
+sont inférieures, ou respectivement supérieure, à la limite $l$, on écrira :

-* $\lim\limits_{x \to \alpha} f(x) = l^-$ ou
+* $\lim\limits_{x \to \alpha} f(x) = l^-$ ou respectivement
 * $\lim\limits_{x \to \alpha} f(x) = l^+$.

 **Exemple** : Préciser les limites à l’infini de la fonction *inverse*.
@@ -275,7 +279,8 @@ r"""$\lim\limits_{x \to -\infty} \frac{1}{x} = 0^-$ et
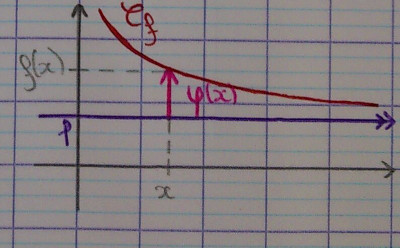
 C’est la distance entre les points de coordonnées $(x, l)$ et $(x, f(x))$,
 c’est-à-dire l’écart entre la droite d’équation $y=l$ et $C_f$, mesuré
 verticalement.  
-Le signe de cet écart est important. On dit que c’est un écart *algébrique*.
+Le signe de cet écart est important. On dit que c’est un écart *algébrique*.  
+Il tend toujours vers 0 (par différence des limites).

 ![phi(x)](img/phi_de_x.jpg)

@@ -465,7 +470,7 @@ $? \circ k$ d’associer $x$ à $x$ (fonction *identité*) ?

 {- spoiler("Réponse",  
 """C’est $k$ elle-même. On dit que $k$ est une involution, comme la fonction
-*opposé*.""") }}
+<em>opposé</em>.""") }}

 #### Théorême

@@ -508,6 +513,11 @@ $x_2 = g(x_1)$. On a :

 À vous de construire un autre exemple.

+#### Remarque
+
+Le théorème peut s’appliquer en une fois même si plus de deux fonctions sont
+composées.
+
 Théorèmes de comparaison
 ------------------------