Lancer le diaporama

1. Additionneur 4 bits avec des portes logiques

Lors d’une formation, j’ai du concevoir un additionneur 4 bits :

• de nombres positifs,
• de relatifs codés en « valeur absolue »,
• de retatifs codés en « biais »,
• de retatifs codés en « complément à deux ».

---

2. Additionneur 4 bits avec des portes logiques

Remarques :

• Les portes sont aux normes états-uniennes, les européennes sont rectangulaires. Voir cette section de l’article Wikipedia correspondant.
• Cette implémentation est personnelle et ne constitue en aucun cas une référence.
• Sans compter la mise en forme, juste les brouillons, on peut compter peut-être une quinzaine d’heures de travail. Merci, c’était très intéressant.

---

3. Addition de positifs

3.1. Deux mots de 1 bit : A11

Retenue se dit carry out en anglais.

Si une retenue sort du mot, on parlera de débordement, ou overflow.

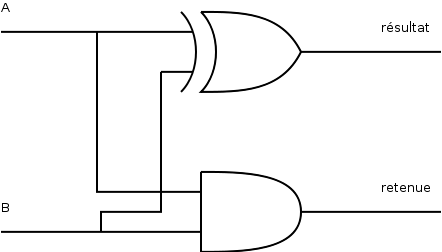
Illustration 1: « A + B = résultat » avec une éventuelle retenue

---

4. Addition de positifs

4.1. Trois mots de 1 bit : A111

But : gérer les retenues.

On peut envisager C (ou toute autre entrée, comme A dans A33 et A44) comme étant une retenue d'un calcul précédent.

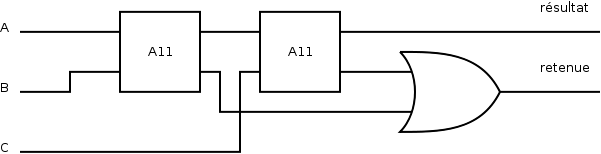
Illustration 2: « A + B + C = résultat » avec une éventuelle retenue

---

5. Addition de positifs

5.1. Deux mots de 3/4 bits : A33/A44

L’addition de mots de 3 bits servira pour les relatifs codés sur 4 bits.

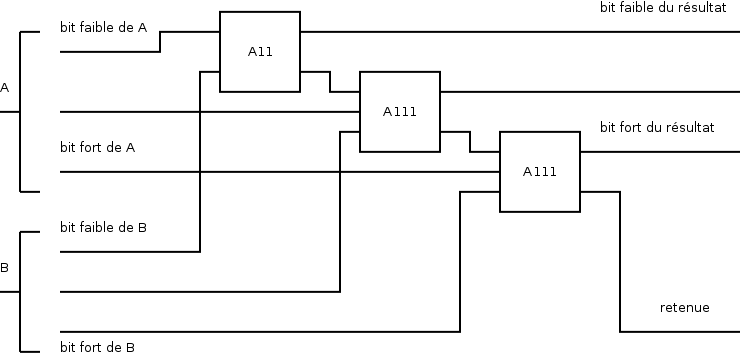
Illustration 3: « A + B = résultat » avec une éventuelle retenue

---

6. Soustraction de positifs

Le codage en « valeur absolue » nous pousse à faire des soustractions pour pouvoir additionner des nombres de signes différent.

---

7. Soustraction de positifs

7.1. Deux mots de 1 bit : S11

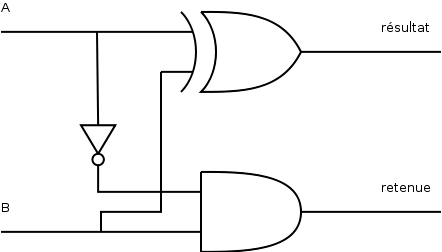
Illustration 4: « A - B = résultat » avec une éventuelle retenue

---

8. Soustraction de positifs

8.1. Trois mots de 1 bit : S111

But : gérer les retenues.

On note la similarité avec A111. On peut encore envisager C (ou toute autre entrée, comme A dans S33) comme étant une retenue d'un calcul précédent.

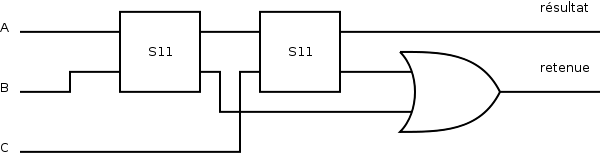
Illustration 5: « A - B - C = résultat » avec une éventuelle retenue

---

9. Soustraction de positifs

9.1. Deux mots de 3 bits : S33

C'est le même schéma que pour A33, en remplaçant respectivement les A11 et A111 par des S11 et S111. La généralisation à des mots plus longs tient toujours.

9.2. Deux mots de 5 bits : S55

Même généralisation qu’à la fin des additionneurs de nombres positifs.

---

10. Comparaison de positifs

10.1. Égalité et comparaison stricte de deux mots de 1 bit : CS11

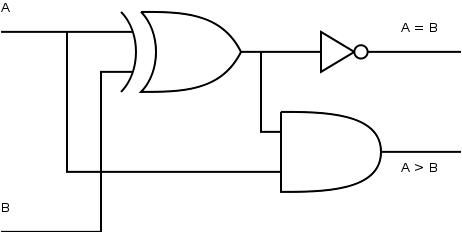
Illustration 6: Comparateur strict à 1 bit

---

11. Comparaison de positifs

11.1. Comparaison large de deux mots de 1 bit : CL11

On retrouve très visuellement :
$(A \geq B) \Leftrightarrow (A \vee \overline B) \Leftrightarrow (\overline B \vee A) \Leftrightarrow (B \Rightarrow A)$, soit $(A \geq B) \Leftrightarrow (B \Rightarrow A)$.

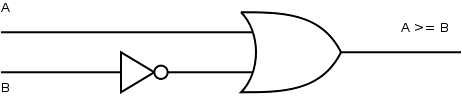
Illustration 7: Comparateur large à 1 bit

---

12. Comparaison de positifs

12.1. Comparaison large de deux mots de 3 bits ou plus : CL33 et CL55

Par récurrence :

Initialisation

On sait comparer des mots de 1 bit avec CL11.

---

13. Comparaison de positifs

Hérédite

En supposant que CL(n-1)(n-1) existe, on a CLnn grâce au schéma suivant :

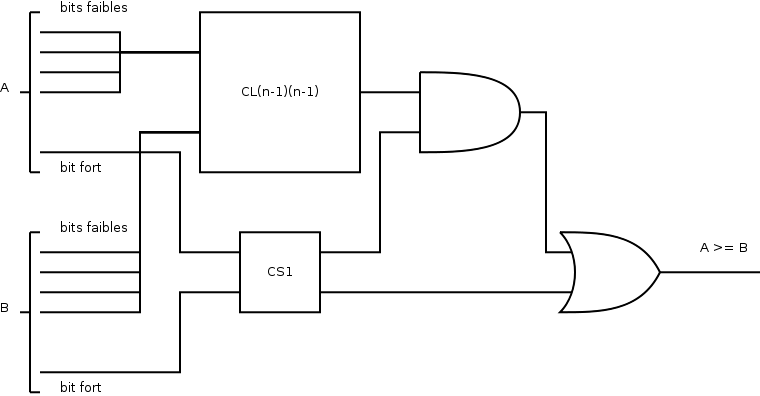
Illustration 8: Comparateur large à n bits

---

14. Gestion du signe de l'addition en codage « valeur absolue » : SG

A + B est négatif dans un des trois cas (incompatibles, mais on utilise deux portes OU pour la disjonction) suivants :

1. A et B sont négatifs,
2. A négatif et B positif, mais $\left| A \right| \geq \left| B \right|$,
3. A positif et B négatif, et $\left| A \right| < \left| B \right|$.

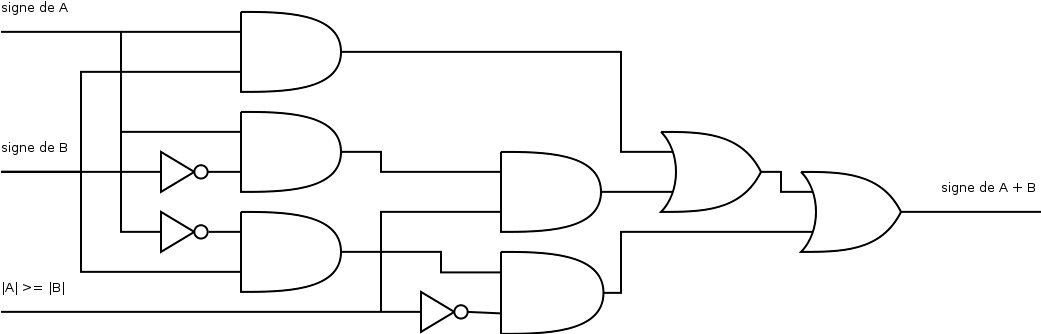
Illustration 9: Gestionnaire du signe d'une addition

---

15. Gestion du débordement de l'addition en « complément à deux » : DC2

Cette opération, réalisée avec un additionneur d'entiers non signés, semble déborder uniquement quand A et B sont de même signe et que le résultat code un nombre de signe opposé. Nous avons donc les deux cas incompatibles (la porte OU) suivants :

1. A et B sont positifs (le NOR), mais le résultat code un nombre négatif,
2. A et B sont négatifs, mais le résultat code un nombre positif.

---

16. Gestion du débordement de l'addition en « complément à deux » : DC2

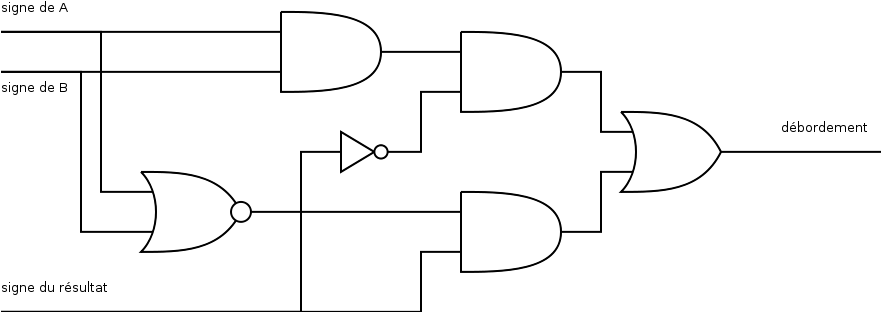
Il me semble que la première phrase aurait permis d'optimiser un peu le circuit…

Illustration 10: Gestionnaire du débordement en complément à deux

---

17. Routage

Par manque de temps, les schémas de cette partie n'ont pu etre réalisés, mais ils sont quasi triviaux.

---

18. Routage

18.1. Multiplexer d'un mot de 1 bit suivant égalite des entrées : XORMUX1

Dirige un bit d'entrée vers une des deux sorties, selon l'egalite de deux autres bits d'entrée. C'est une sorte d'aiguillage, qui nous sert pour l'addition en codage « valeur absolue » afin d'orienter vers une addition ou une soustraction des valeurs absolues.

---

19. Routage

19.1. Multiplexer d'un mot de 3 bits suivant égalite des entrées : XORMUX3

Généralisation de XORMUX1 par récurrence (voir CL33 en III 3). Sur trois bits uniquement car les mots de 4 bits ont leur valeur absolue codée sur 3 bits.

---

20. Routage

20.1. Merger M3

Sorte de porte OU géante ou 2 mots de 3 bits entrent, mais un seul sort.

---

21. Routage

21.1. Switcher SW3

Échange deux mots de trois bits suivant la valeur d'un bit. C'est une sorte d'aiguillage, qui nous sert pour l'addition en codage « valeur absolue » afin de soustraire les valeurs absolues dans le bon sens.

---

22. Addition de relatifs

Synthèse des éléments vus précédemment.

---

23. Addition de relatifs

23.1. En codage « valeur absolue »

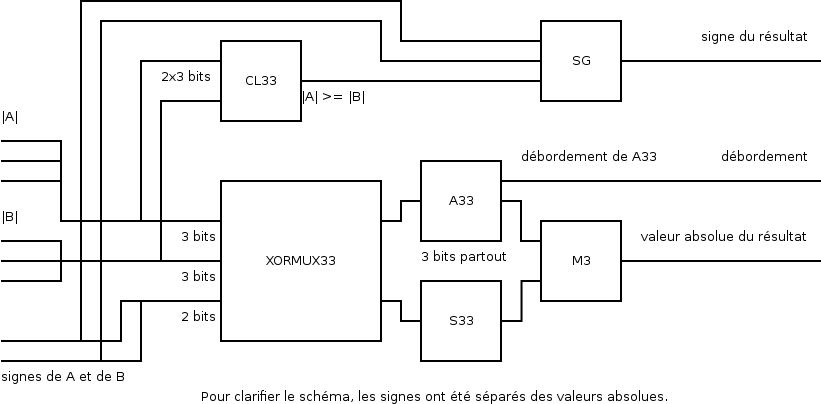
Illustration 11: Additionneur 4 bits avec codage « valeur absolue »

---

24. Addition de relatifs

24.1. En codage « biais »

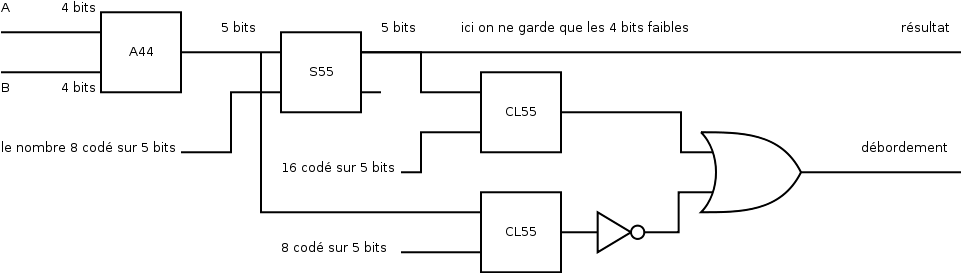
Illustration 12: Additionneur 4 bits avec codage « biais »

---

25. Addition de relatifs

25.1. En codage « complément à deux »

On comprend ici l’intérêt de cette façon de coder les négatifs.

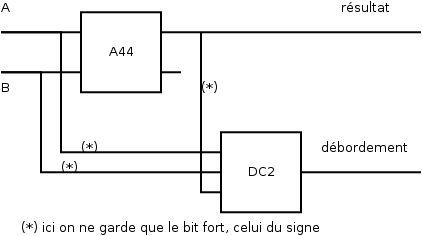
Illustration 13: Additionneur 4 bits avec codage « complément à deux »

---

26. Conclusion

Ces implémentations possibles rendent compte de la taille de l’ongle du petit doigt de la partie émergée de la complexité d’un processeur. Quelques liens pour approfondir :

• l’article Wikipedia sur les additionneurs
• la recherche d’images sur Google
• les tableaux de Karnaugh permettent justement de trouver les expressions logiques qui se cachent derrière une table de vérité (ici à 8 entrées, donc 256 lignes).
• l’implémentation avec le démineur
• l’implémentation avec Minecraft
• d’autres mécanismes de ce genre avec Minecraft
• …

Tweeter Suivre @profgraorg