tite fractale

Systèmes de numération

1. Un peu d’histoire

L’histoire des numérations est longue et riche. On peut noter :

Rappelons qu’ici on ne parle que des entiers. Les ensembles de nombres qui contiennent les entiers : $$\mathbb N \subset \mathbb Z\ \subset \mathbb D \subset \mathbb Q \subset \mathbb R \subset \mathbb C \subset \mathbb H \subset \mathbb O \subset \mathbb S$$ ont aussi une histoire très riche. Cette histoire, plus récente, continue cependant de s’écrire encore aujourd’hui, grâce à la recherche en mathématique (voir sur Wikipedia les articles sur les nombres p-adiques et Oméga de Chaitin).

Nous étudions ici des numérations de positions. Un chiffre n’a pas la même valeur suivant l’endroit où il est placé dans le nombre, contrairement par exemple aux nombres romains. C’est bien plus pratique pour conduire des opérations, que ce soit à la main ou avec des machines. Beaucoup de mécanismes d’une base peuvent même être utilisés dans d’autres.

2. Les bases de la numération occidentale

2.1. Nombre et chiffre

2.1.1. Nombre

La notion de nombre étant difficile à définir précisément à notre niveau, on la considère acquise.

2.1.2. Chiffre

Un chiffre est un symbole utilisé pour écrire un nombre. Un nombre peut s’écrire à l’aide d’un ou de plusieurs chiffres.

2.1.3. Exemple

Lequel de ces chiffres est le plus grand ? Lequel de ces nombres est le plus grand ?

2    4

2.2. Les bases les plus courantes

2.2.1. La base trois

2.2.1.1. Le berger

Considérons un berger qui ne sait compter que jusqu’à trois et son troupeau de 17 moutons.

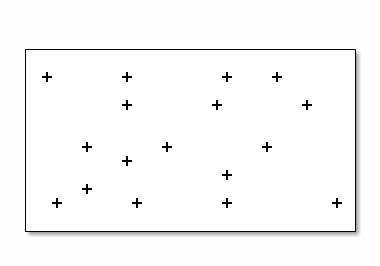
ditaa diagram

2.2.1.1.1. Paquets de trois moutons

Dès qu’il arrive à 3 moutons, il en fait un paquet. Soit 5 paquets puisque 17=5×3+2. Il reste 2 moutons.

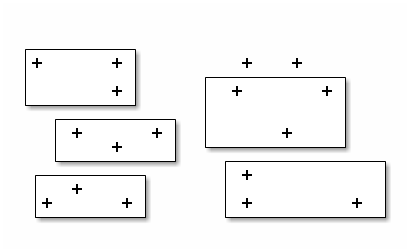
ditaa diagram

2.2.1.1.2. Division euclidienne

La division euclidienne est justement l’écriture d’un nombre entier en paquets, avec un éventuel reste.

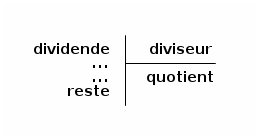
Définition

On admet que pour tout entier $n$ et tout entier non nul $d$, il existe un unique couple d’entiers $q$ et $r$ tel que :

$$\left\{ \begin{array}{l} n = d × q + r \\\\ 0 \le r < d \end{array} \right.$$

On dira que l’on a effectué, ou écrit, la division euclidienne de n par d.

ditaa diagram

Exemple

139 = 15×7 + 6

On peut obtenir ce résultat de plusieurs façons :

Voici quelques exercices de calcul de restes à faire mentalement.

Attention  Ne pas écrire de division à l’aide d’une fraction ou du symbole ÷. Toujours utiliser $n = q × d + r$, même si cette égalité peut décrire deux divisions.

2.2.1.1.3. Paquets de trois paquets de trois

Puis des paquets de trois « paquets de trois ». Ici on ne considère plus les moutons restés seuls à l’étape précédente. On a 1 paquet de trois (paquets de trois) et il en reste 2 (paquets de trois), puisque 5=1×3+2.

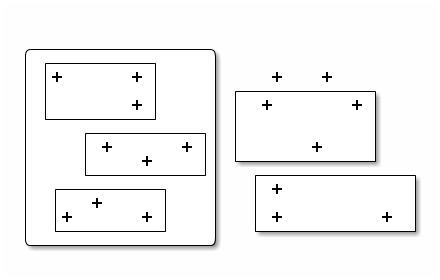
ditaa diagram

Ensuite, il faut voir si on peut regrouper en paquets de paquets de paquets. Comme 1 est strictement plus petit que 3, le quotient par 3 est nul : 1=0×3+1. Trouver « 0 » au quotient indique qu’il n’y aura plus de paquets d’ordre supérieur à faire.

Tant que le quotient n’est pas nul, on continue avec des paquets de paquets de paquets de paquets de paquets de paquets…

2.2.1.1.4. Écriture de 17 en base 3

En écrivant les restes de droite à gauche, on obtient « 122 », que l’on notera entre parenthèses et avec un indice pour préciser la taille des paquets utilisés : $(122)_3$.

D’où l’importance de la position. Les trois chiffres n’ont pas le même « poids » suivant leur position.

La quatrième position aurait compté les paquets de paquets de paquets, soit 3×3×3 moutons.

Plutôt que d’écrire une suite de multiplications avec que des 3, on utilise la notation puissance :

$$ \begin{aligned} 17 &= 5×3 + 2 &(1) \\\\ &= (1×3 + 2)×3 + 2 &(2) \\\\ &= 1×3^{2} + 2×3^1 + 2×3^0 &(3) \\\\ \end{aligned} $$

  1. Division euclidienne de 17 par 3.
  2. Division euclidienne de 5 par 3.
  3. On développe les multiplications par 3, sachant que 31 vaut 3 et 30 vaut 1.

2.2.1.2. Présentation des calculs sur un autre exemple

Il y a, entre autres, trois façons de mener les calculs. Elles ont en commun l’utilisation de la division euclidienne, dont on ne peut se passer. Dans tous les cas, on trouvera bien $59 = (2012)_3$.

2.2.1.2.1. Avec les parenthèses

$$ \begin{aligned} 59 &= 19×3 + 2 \\\\ &= (6×3 + 1)×3 + 2 \\\\ &= ((2×3 + 0)×3 + 1)×3 + 2 \\\\ &= (((0×3 + \mathbf{2})×3 + \mathbf{0})×3 + \mathbf{1})×3 + \mathbf{2} \\\\ \end{aligned} $$

La présentation est fastidieuse, mais l’égalité mathématique est respectée d’une ligne à une autre. La lecture se fait naturellement de gauche à droite puisque les derniers restes, qui ont le poids fort, sont à gauche.

2.2.1.2.2. En écrivant seulement les quotients successifs

$$ \begin{aligned} 59 &= 19×3 + 2 \\\\ 19 &= 6×3 + 1 \\\\ 6 &= 2×3 + 0 \\\\ 2 &= 0×3 + 2 \\\\ \end{aligned} $$

Attention, la lecture se fait de bas en haut puisque les derniers restes, qui ont le poids fort, sont en bas.

2.2.1.2.3. En présentant les divisions à l’ancienne (avec les barres)

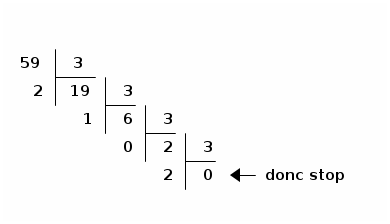
ditaa diagram

Attention, la lecture se fait de bas en haut puisque les derniers restes, qui ont le poids fort, sont en bas.

2.2.1.3. Remarques

  1. En base 3, on utilise 3 chiffres : 0, 1 et 2. Pas besoin de plus, sinon on aurait pu faire un paquet de trois et l’écrire dans la colonne juste à gauche.
  2. On peut déja comprendre (mais vous le verrez en faisant les exercices suivants), que les nombres écrits en base 3 sont plus longs qu’en base 10, même s’ils décrivent la même quantité. On fait plus de paquets de 3 que de paquets de 10, et ont doit donc plus changer de colonne.
  3. Attention aux restes nuls, qui doivent être représentés dans le nombre final par des zéros afin que les restes suivants soient bien dans la colonne qui correspond à leur poids.

2.2.1.4. Exercices

Quels nombres représentent $(1)_3$, $(10)_3$, $(100)_3$, $(1000)_3$, $(1201)_3$, $(110221)_3$ ?

Comment représenter 1 en base 3 ? Même question pour 4, 10, 100, 1984 en base 3.

2.2.2. Égalités fondamentales

$$(10)_a = a$$

$$(1\underbrace{0....0}_{n~\text{zéros}})_a = a^n$$

2.2.3. La base dix

La morphologie humaine est sans doute la cause de notre utilisation de la base 10, appelé « système décimal ». Notons que les puissances de 3 deviennent les puissances de 10, soit les unités, les dizaines, les centaines… On a mis du temps à le comprendre en primaire, mais les positions ont bien différents poids.

Ce système a besoin des 10 chiffres que nous connaissons bien, les chiffres dits « arabes », en fait inventés en Inde. Nous les connaissons tellement bien cette base que les égalités fondamentales y sont évidentes.

Pour plus de détails, voir l’article sur Wikipedia.

2.2.4. Le binaire

2.2.4.1. Raison de son utilisation

L’architecture matérielle des systèmes informatiques actuels est basée sur des phénomènes physiques à deux états :

Par convention, on représentera un de ces états par un 0, et l’autre par un 1.

Grâce à ces deux valeurs, en comptant en base 2 et en s’organisant bien, on peut représenter beaucoup d’entiers, des grands, et même bien plus de choses encore.

2.2.4.2. Le berger à deux doigts

Exercice : Comment écrit-on le nombre 27 en base 2 ?

2.2.4.3. Vocabulaire

2.2.4.4. Remarques et exercices

2.2.5. L’hexadécimal

2.2.5.1. Définitions

Comme les mots binaires sont très longs, les humains ne peuvent pas utiliser directement la base 2. La base 10 n’est pas pratique non plus car le travail de conversion n’est pas très simple. Comme 8 et 16 sont des puissances de 2, ce sont des bases plus pratiques pour parler et écrire à propos des ordinateurs, ou même « avec » les ordinateurs.

Le système en base 8 s’appelle l’octal mais n’est plus très utilisé.

La représentation d’un nombre en hexadécimal, ou en « hexa » pour les intimes, est son écriture en base 16. Ainsi, nous avons besoin de 16 chiffres ! Les 6 manquants ont été choisis ainsi : A, B, C, D, E et F.

2.2.5.2. Remarques et exercices

Technique

En base 16, peu de chiffres suffisent à écrire des nombres très grands (chaque chiffre en hexa « pèse » une puissance de 16). Quels nombres représentent $(1)_{16}$, $(10)_{16}$, $(100)_{16}$, $(1000)_{16}$, $(1789)_{16}$, $(1984)_{16}$, $(FFFF)_{16}$ ?

Comment représenter 1 en base 16 ? Même question pour 4, 10, 15, 16, 100, 1024, 1789, 1984, 220.

Quartets

Comme 16 est une puissance de 2, les liens entre le binaire et l’hexa sont très forts. Exprimer les puissances de 16 en puissances de 2. On rappelle cette égalité concernant les puissances : $$\left(\left(a\right)^m\right)^n = \left(a\right)^{m×n}$$

On remarque que les puissances de 16 peuvent être obtenues en extrayant une puissance de 2 sur quatre. Ce qui explique que :
« En hexadécimal, un seul chiffre code un quartet ».

Écrire une table de conversion hexa-décimal-binaire pour tous les quartets.

Octets

De combien de chiffres hexa a-t-on besoin pour coder un octet ? Écrire une table de conversion décimal-hexa-binaire pour les octets les plus célèbres.

Synthèse

Cette activité résume les calculs qu’il faut savoir faire. On remarque que pour les conversions directes de binaire en hexa ou inversement, il suffit de savoir convertir quartet par quartet.

3. Opérations

3.1. Le ET logique

Si on se donne deux mots binaires de même longueur, le résultat de cette opération reste un mot de même longueur. On note :

'mot1' & 'mot2' = résultat

Le caractère s’appelle esperluette et sera prononcé ici « et ». Le résultat est défini comme suit…

3.1.1. Deux mots de 1 bit

0 & 0 = 0 ;      0 & 1 = 0 ;      1 & 0 = 0 ;      1 & 1 = 1

3.1.1.1. Remarques

On retrouve cette idée en logique des propositions, en logique booléenne, en électronique et en électricité.

3.1.2. Mots de plus de 1 bit

On raisonne avec les bits de même poids face à face, pour reconstituer le résultat.

3.1.2.1. Exemple

$$ \begin{aligned} (240)_{10} \& (154)_{10} &= (1111 0000)_2 \& (1001 1010)_2 &1)\\\\ &= (1001 0000)_2 &2)\\\\ &= (144)_{10} &3) \end{aligned} $$

1) et 3) conversions décimal -> binaire ou binaire -> décimal

2)

1111 0000
1001 1010
---------
1001 0000

3.1.2.2. Remarques

    1000 0000        0000 0001
    1100 0000        0000 0011
    1110 0000        0000 0111
    1111 0000        0000 1111
    1111 1000        0001 1111
    1111 1100        0011 1111
    1111 1110        0111 1111
    1111 1111        1111 1111

3.1.2.3. Exemples fondamentaux

Pour n’importe quel octet x,

0 & x = 0
255 & x = x

3.2. Les opérations usuelles, mais en binaire

3.2.1. Généralités

Elles se comportent comme en base 10. Les problèmes auxquels nous devont faire face sont dus :

Il est possible de vérifier son résultat en :

  1. convertissant en décimal,
  2. effectuant l’opération en décimal,
  3. convertissant le résultat en binaire.

3.2.2. Exemples

3.2.2.1. Addition

      101
    +1110
    -----

      101
    +1110
    -----
    10011

3.2.2.2. Soustraction

     1011
     -101
     ----

     1011
     -101
     ----
     0110

3.2.2.3. Multiplication

      111
    ×1101
    -----

      111
    ×1101
    -----
      111
     000.
    111..
  +111...
  -------
  1011011

3.2.2.4. Division


10101 | 11
      |----
      |
      |
      |
      |

---
10101 | 11
-11   |----
---   | 111
 100  |
 -11  |
 ---  |
   11 |
  -11 |
  --- |
    0 |

Aller aux exercices




Christophe Gragnic, le 26/09/2014, 15h05'58".






Page générée le 27/05/2021, 09h06'59" (source).
historique de la page
historique global