1. Introduction

Il est important d’avoir bien compris le chapitre précédent avant d’attaquer celui-ci.

Dans ce chapitre, on notera :

• $\alpha$ un nombre réel $x_0$ ou $-\infty$ ou $+\infty$.
• $I$ un intervalle de la forme :
  • $\left] x_0 - h ; x_0 + h \right[$ si $\alpha = x_0$, où $h > 0$ (on note que l’intervalle est centré autour de $x_0$),
  • $\left] -\infty ; A \right[ $ si $\alpha = -\infty$, où $A \in \mathbb R$,
  • $\left] A ; +\infty \right[ $ si $\alpha = +\infty$, où $A \in \mathbb R$.
  • On dira que $I$ est un voisinage de $\alpha$.
• $f$ une fonction au moins définie sur un intervalle $I$ : $I \subset D_f$
• $C_f$ la représentation graphique de $f$.

On appellera :

• « petit nombre (réel) » un nombre proche de 0 (et non un grand nombre négatif);
• « grand nombre (réel) positif » et « grand nombre (réel) négatif » des nombres dont la valeur absolue est grande;
• « grand nombre (réel) » un grand nombre réel, positif ou négatif.

Même si ces tailles ne sont pas définies plus précisément, cela nous aidera à comprendre certains mécanismes.

2. Limites finies

2.1. Définition générale

On dit que la limite de $f$ en $\alpha$ est égale au réel $l$ si :

pour tout $\epsilon > 0$, $x$ proche de $\alpha$ entraîne $f(x) \in \left] l - \epsilon ; l + \epsilon \right[$.

On notera $\lim\limits_{x \to \alpha} f(x) = l$ ou parfois simplement $\lim\limits_{\alpha} f = l$ si la fonction a un nom.

On dira indifféremment :

• « $f(x)$ tend vers $l$ quand $x$ tend vers $\alpha$ »
• « $f$ tend vers $l$ en $\alpha$ »
• « la limite de $f(x)$ quand $x$ tend vers $\alpha$ vaut $l$ »
• « la limite de $f$ en $\alpha$ vaut $l$ »

2.2. Trois cas particuliers

2.2.1. $\alpha = x_0$

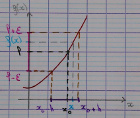
« $x$ proche de $x_0$ » signifie « il existe un $h$ tel que $x \in \left] x_0 - h ; x_0 + h \right[$».

Le rôle de $\epsilon$ est d’être petit, et $h$ sera en général contraint à être petit aussi.

Exemple : $\lim\limits_{x \to 3} x^2 = 9$ (voir plus loin la notion de continuité).

2.2.2. $\alpha = +\infty$

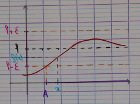
« $x$ proche de $+\infty$ » signifie « il existe un $A$ tel que $x \ge A$».

Le rôle de $\epsilon$ est d’être petit, et $A$ sera en général contraint à être un grand nombre positif.

Exemple : $\lim\limits_{x \to +\infty} \frac{1}{x} = 0$

2.2.3. $\alpha = -\infty$

« $x$ proche de $-\infty$ » signifie « il existe un $A$ tel que $x \ge A$».

Le rôle de $\epsilon$ est d’être petit, et $A$ sera en général contraint à être un grand nombre négatif.

Exemple : $\lim\limits_{x \to -\infty} \frac{1}{x} = 0$

3. Limites infinies

3.1. Limites égales à $+\infty$

3.1.1. Définition

On dit que $f$ tend vers $+\infty$ lorsque tout intervalle de la forme $\left]M;+\infty\right[$ où $M$ est un réel, contient $f(x)$ pour $x$ suffisamment proche de $\alpha$.

Autrement dit, pour tout nombre réel $M$ (destiné à être un grand nombre), il existe un voisinage de $\alpha$ dans lequel tout $x$ est tel que $f(x) > M$.

On notera $\lim\limits_{x \to \alpha} f(x) = +\infty$ ou parfois simplement $\lim\limits_{\alpha} f = +\infty$ si la fonction a un nom.

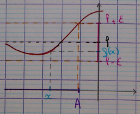
3.1.2. $\alpha = +\infty$

Pour tout nombre réel $M$ (destiné à être un grand nombre positif), il existe un réel $A$ (qui sera aussi amené à être un grand nombre positif), à partir duquel toutes les images par $f$ sont supérieures à $M$, c’est-à-dire que si $x > A$, alors $f(x) > M$.

3.1.3. $\alpha = -\infty$

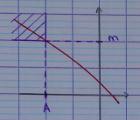
Pour tout nombre réel $M$ (destiné à être un grand nombre positif), il existe un réel $A$ (qui sera cette fois amené à être un grand nombre négatif), à partir duquel toutes les images par $f$ sont supérieures à $M$, c’est-à-dire que si $x < A$, alors $f(x) > M$.

3.1.4. $\alpha = x_0$

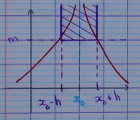
Le rôle de $M$ est d’être un grand nombre positif, et $h$ sera en général contraint à être un petit nombre.

Exemple : Soit $f$ la fonction définie sur $\left] -\infty; 1 \right[ \cup \left]1; +\infty \right[$ par $f(x) = \frac{3}{(x-1)^2}$.

1) À l’aide de la calculatrice, trouver le $x_0$ où la limite de $f$ est infinie.
2) Montrer que : $\lim\limits_{x \to 1} f(x) = +\infty$.

Proposition de réponses :

1) Il suffit de trouver la bonne fenêtre d’étude, c’est-à-dire bien régler Xmin, Xmax, Ymin et Ymax.

2) Montrons que : $\lim\limits_{x \to 1} f(x) = +\infty$ Soit $M$ un nombre réel. Cherchons un réel $h$ strictement positif tel que :

« si $x \in \left] 1 - h ; 1 + h \right[$ alors $f(x) > M$. »

Résolvons donc cette dernière inéquation en $x$ ($M$ étant donné).

Premier cas : $M \le 0$

Comme $f$ est strictement positive sur son domaine de définition, si le $M$ donné est négatif, tout $h$ convient pour que l'égalité soit vraie.

Deuxième cas : $M > 0$

$$ \begin{aligned} f(x) &> M &(1) \\\\ \frac{3}{(x-1)^2} &> M &(2) \\\\ \frac{1}{(x-1)^2} &> \frac{M}{3} &(3) \\\\ (x-1)^2 &< \frac{3}{M} &(4) \\\\ |x-1| &< \sqrt{\frac{3}{M}} &(5) \\\\ -\sqrt{\frac{3}{M}} < x &- 1 < \sqrt{\frac{3}{M}} &(6) \\\\ 1 - \sqrt{\frac{3}{M}} < x & < 1 + \sqrt{\frac{3}{M}} &(7) \\\\ \end{aligned}$$

1. Équation de départ.
2. Expression de $f$.
3. On divise les deux membres par 3.
4. La fonction inverse est décroissante sur $\mathbb R_+^* = \left] 0; +\infty \right[$.
5. On utilise le cours de seconde, $\frac{3}{M}$ étant positif.
6. Pour ceux qui ne connaissent pas la valeur absolue.
7. On ajoute 1 aux deux membres.

On note que les étapes (4) et (5) n'auraient pas pu être réalisées dans le cas $M \le 0$.

Finalement, le $h$ cherché est $\sqrt{\frac{3}{M}}$.

Calculer par exemple le $h$ correspondant à $M = 10^6$ et vérifier graphiquement à la calculatrice.

3.1.5. Remarque importante

$-\infty$ et $+\infty$ ne participent pas à des calculs comme les autres nombres.

3.2. Limites égales à $-\infty$

Idem, mais le rôle de $M$ sera d’être un grand nombre négatif, et les images de $f$ devront lui être inférieures.

4. Précisions horizontales et verticales sur les limites

4.1. Limite à gauche et limite à droite

Lorsque $\alpha$ est fini ($\alpha = x_0$) et que l’on ne s’intéresse qu’aux valeurs de $f(x)$ pour les $x$ « restant du même côté de $x_0$ », on écrira :

• $\lim\limits_{\underset{x < x_0}{x \to x_0 }} f(x)$ ou
• $\lim\limits_{\underset{x > x_0}{x \to x_0 }} f(x)$.

On pourra écrire aussi, respectivement :

• $\lim\limits_{x \to x_0^-} f(x)$ ou
• $\lim\limits_{x \to x_0^+} f(x)$.

Remarques :

• On parlera respectivement de « limite à gauche de $x_0$ » et de « limite à droite de $x_0$ ».
• Le petit signe + ou - n’a aucun rapport avec le signe de $x_0$, sauf bien sûr si $x_0 = 0$.

Exemple : Donner les limites autour de 0 de la fonction inverse.

4.2. Comparaison de f avec sa limite

Lorsque $f$ a une limite finie $l$ en $\alpha$ où $\alpha = -\infty$ ou $\alpha = +\infty$ et que, au voisinage de $\alpha$, les images par $f$ sont inférieures, ou respectivement supérieure, à la limite $l$, on écrira :

• $\lim\limits_{x \to \alpha} f(x) = l^-$ ou respectivement
• $\lim\limits_{x \to \alpha} f(x) = l^+$.

Exemple : Préciser les limites à l’infini de la fonction inverse.

Remarque : Il est pratique de poser $\phi (x) = f(x) - l$.
C’est la distance entre les points de coordonnées $(x, l)$ et $(x, f(x))$, c’est-à-dire l’écart entre la droite d’équation $y=l$ et $C_f$, mesuré verticalement.
Le signe de cet écart est important. On dit que c’est un écart algébrique.
Il tend toujours vers 0 (par différence des limites).

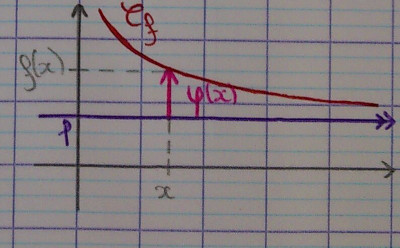
Cette nouvelle notation pour la limite $l$ s'utilise donc quand le signe de $\phi (x)$ est constant pour $x$ restant proche de $\alpha$.

4.3. Exemples

Donner les limites de la fonction inverse aux bornes de son ensemble de définition. Penser à utiliser les nouvelles notations. Même question avec la fonction $f$ définie par $f(x) = \frac{1 - 5x}{4x - 3}$.

5. Conséquences sur l’étude d’une fonction

5.1. Limites dans le tableau de variation

5.2. Interprétations graphiques

5.2.1. Asymptotes verticales

5.2.1.1. Définition

Lorsque l'un des cas suivants est vérifié :

• $\lim\limits_{\underset{x < x_0}{x \to x_0 }} f(x) = - \infty$
• $\lim\limits_{\underset{x < x_0}{x \to x_0 }} f(x) = + \infty$
• $\lim\limits_{\underset{x > x_0}{x \to x_0 }} f(x) = - \infty$
• $\lim\limits_{\underset{x > x_0}{x \to x_0 }} f(x) = + \infty$

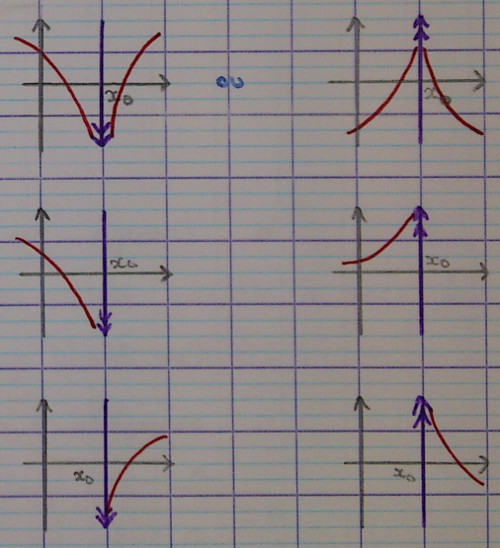
on dira que la droite d'équation $x=x_0$ est asymptote à $C_f$. On la représentera avec le codage de la double flèche, sans forcément trop la prolonger.

5.2.1.2. Remarque

On dit parfois abusivement asymptote verticale, mais on devrait dire parallèle à l'axe des ordonnées.

5.2.1.3. Exemples et contre-exemples

L'axe des ordonnées est asymptote à l'hyperbole de référence, mais la parabole de référence n'a pas d'asymptote.

5.2.2. Asymptotes horizontales

5.2.2.1. Définition

Lorsque l'un des cas suivants est vérifié :

• $\lim\limits_{x \to -\infty} f(x) = l$
• $\lim\limits_{x \to +\infty} f(x) = l$

on dira que la droite d'équation $y=l$ est asymptote à $C_f$. On la représentera avec le codage de la double flèche, sans forcément trop la prolonger.

En reprenant la notation $\phi (x) = f(x) - l$, ces cas s'écrivent :

• $\lim\limits_{x \to -\infty} \phi (x) = 0$
• $\lim\limits_{x \to +\infty} \phi (x) = 0$

Attention, il n'y a pas de contrainte sur le signe de $\phi (x)$ quand $x$ est grand. Il peut être négatif, positif ou ne pas être constant.

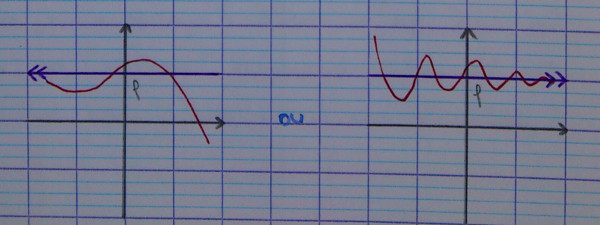
5.2.2.2. Remarque

On dit parfois abusivement asymptote horizontale, mais on devrait dire parallèle à l'axe des abscisses.

5.2.2.3. Exemples et contre-exemples

L'axe des abscisses est asymptote à l'hyperbole de référence, mais la courbe représentative de la fonction racine carrée n'a pas d'asymptote.

5.2.3. Doubles asymptotes

Attention, certaines droites peuvent être asymptotes à une courbe « de deux côtés », c'est-à-dire à droite et à gauche de $x_0$ pour une asymptote verticale, et en $-\infty$ ou $+\infty$ pour les asymptotes horizontales.

C'est le cas bien sûr des axes du repère pour l'hyperbole de référence.

5.2.4. Étude de positions relatives

Soit $f$ une fonction dont la courbe représentative $C_f$ admet la droite $\mathscr D$ d'équation $y=l$ pour asymptote.

On reprend encore la notation $\phi (x) = f(x) - l$.

Le signe de $\phi$ nous donne des indications sur les positions relatives de $C_f$ et $\mathscr D$ de la façon suivante :

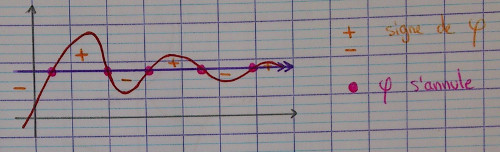
Pour répondre à la question « donner la position relative de la courbe par rapport à son asymptote », un tableau peu parfois être très efficace, un peu comme lors d'une étude des variations.

6. Calculs de limites

6.1. Absence de limite

6.1.1. Incohérence à droite et à gauche

Dans le cas où $\alpha = x_0$, si les limites à gauche et à droite de $x_0$ existent mais sont différentes, on dira qu’il n’y a pas de limite en $x_0$.

C’est le cas de la fonction inverse en 0.

6.1.2. Autres cas

De la même manière que pour les suites, on peut trouver des fonctions qui ont le mauvais goût de ne pas avoir de limite.

sin cos

On peut même trouver pire : des fonctions n'ayant pas de limite en un réel fini. Il suffit de composer à droite avec la fonction inverse pour amener l'infini en zéro. C'est par exemple le cas de la fonction $f$ définie sur $\mathbb R_+^*$ par $f(x) = sin \left( \frac{\pi}{x} \right)$, mais on peut trouver des monstres bien plus terribles…

6.2. Opérations sur les fonctions

6.2.1. Celles des nombres

Ce sont les mêmes règles que pour les suites.

Voir le tableau et les exemples du livre.

Attention, pour les limites de fonctions polynômes et rationnelles, on applique les propriétés des termes de plus haut degré uniquement en l’infini (se remémorer les démonstrations si besoin).

6.2.2. Limites de fonctions composées

6.2.2.1. Rappel

La composition est une opération qui n’existe pas chez les nombres. Elle consiste simplement à créer une nouvelle fonction à partir de l'enchaînement de deux fonctions. Sans parler des ensembles de définition, on a :

$$(f \circ g) (x) = f \circ g (x) = f(g(x))$$

Que l’on prononce « f rond g » et que l’on représente par les diagrammes suivants :

$$ x \overset{g}{\longmapsto} g(x) \overset{f}{\longmapsto} f\left(g\left(x\right)\right) $$

Ou plus généralement, où les lettres minuscules sont des nombres, les majuscules des ensembles :

$$A \overset{g}{\longrightarrow} B \overset{f}{\longrightarrow} \Gamma$$

$$\alpha \overset{g}{\longmapsto} \beta \overset{f}{\longmapsto} \gamma$$

Exemples et exercices :

1) En notant $f$, $g$, $h$, $k$ les fonctions définies par :

• $f(x) = x + 1$;
• $g(x) = x^2$;
• $h(x) = \sqrt x$;
• $k(x) = \frac{1}{x}$.

Écrire l’image de $x$ par les fonctions suivantes. Vous écrirez tout d’abord cette image sans simplification, puis avec :

• $f \circ g$
• $g \circ f$
• $g \circ h$ et $h \circ g$
• $f \circ k$ et $k \circ f$
• … (le reste des composées, pour l’instant sans $f \circ f$, $g \circ g$, $h \circ h$ ni $k \circ k$)

La composition est-elle commutative ?

2) Quelle est la fonction mystère qui permet à $k \circ ?$ et à $? \circ k$ d’associer $x$ à $x$ (fonction identité) ?

6.2.2.2. Théorême

Soient $f$, $g$ et $h$ trois fonctions telles que pour $x \in D_f$, $f(x) = h \circ g (x) = h(g(x))$, et $\alpha$, $\beta$ et $\gamma$ des nombres finis ou infinis.

Si $\lim\limits_{x \to \alpha} g(x) = \beta$ et $\lim\limits_{x \to \beta} h(x) = \gamma$, alors $\lim\limits_{x \to \alpha} f(x) = \gamma$.

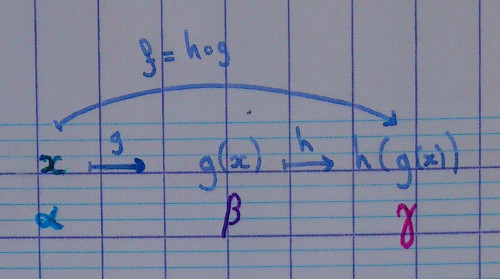
6.2.2.3. Exemple

Soit $f$ la fonction définie sur $\mathbb R ^{+*}$ par $f(x) = \sqrt{\frac{1}{x} + 2}$.
Pour déterminer la limite de f en $+\infty$, on décompose la fonction $f$ en appliquant :

• d’abord la fonction $g \colon x_1 \longmapsto g(x_1) = \frac{1}{x_1} + 2$,
• puis la fonction racine, ici notée $h$, c’est-à-dire $h \colon x_2 \longmapsto h(x_2) = \sqrt x_2$.

La composition des deux fonctions $f = h \circ g$ peut en quelque sorte s’écrire $x_2 = g(x_1)$. On a :

• tout d'abord $\lim\limits_{x \to +\infty} g(x) = 2$ (opérations sur les limites),
• puis $\lim\limits_{x \to 2} h(x) = 2$ (car $h$ est continue, voir plus loin),
• finalement, $\lim\limits_{x \to +\infty} f(x) = \sqrt{2}$. Voici le diagramme final : $$+\infty \overset{g}{\longmapsto} 2 \overset{h}{\longmapsto} \sqrt 2$$

À vous de construire un autre exemple.

6.2.2.4. Remarque

Le théorème peut s’appliquer en une fois même si plus de deux fonctions sont composées.

6.3. Théorèmes de comparaison

6.3.1. Théorème du Sumo

6.3.1.1. Remarque préliminaire

Attention, cette dénomination n'est pas officielle. On utilise plus souvent, classiquement et (trop) simplement la dénomination « théorème de comparaison ».

6.3.1.2. Théorème

Soit $f$ et $g$ deux fonctions définies sur un intervalle $I$, voisinage de $\alpha$ (où $\alpha = x_0$ ou $-\infty$ ou $+\infty$). Revoir l'introduction pour ces notations et la notion de voisinage.

• Si pour tout $x$ de $I$ on a $g(x) \le f(x)$ et si $\lim\limits_{x \to \alpha} g(x) = +\infty$, alors $\lim\limits_{x \to \alpha} f(x) = +\infty$.
• De même, si pour tout $x$ de $I$ on a $g(x) \ge f(x)$ et si $\lim\limits_{x \to \alpha} g(x) = -\infty$, alors $\lim\limits_{x \to \alpha} f(x) = -\infty$.

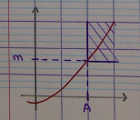
Voici le schéma pour le cas $\alpha = +\infty$ et $\lim\limits_{x \to \alpha} g(x) = +\infty$.

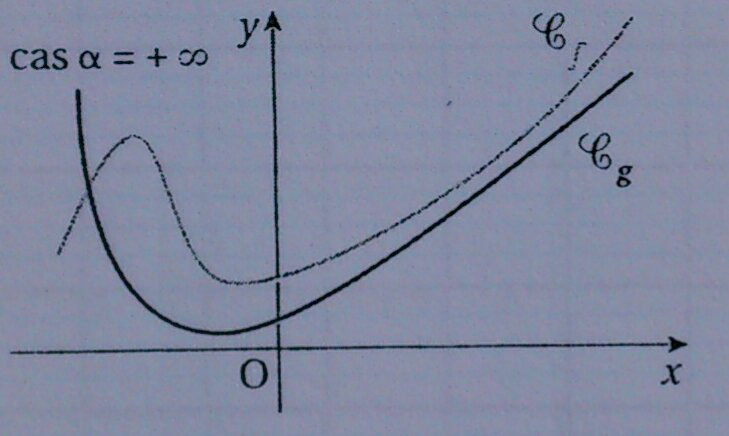
Combien reste-t-il de schémas à faire ?

6.3.1.3. Démonstration

On ne démontre que le cas $\alpha = +\infty$ et $\lim\limits_{x \to \alpha} g(x) = +\infty$. Les autres démonstrations sont très similaires.

Soit un réel $M$. Cherchons un réel $A$ tel que pour tout $x > A$, $f(x) > M$ (voir la définition d'une limite infinie).

D'une part, sur $I$, de la forme $\left] A', +\infty \right[$, $f$ est supérieure à $g$. Donc pour $x > A'$, $f(x) > g(x)$.

D'autre part, $\lim\limits_{x \to \alpha} g(x) = +\infty$, donc il existe un réel, noté ici $A''$, tel que pour tout $x > A''$, $g(x) > M$.

Il suffit donc de prendre $A = max(A', A'')$, car si $x > A$, on a à la fois $x > A'$ et $x > A''$, et donc :

$$f(x) > g(x) > M$$

6.3.2. Théorème des gendarmes

6.3.2.1. Remarque

Cette dénomination est très courante, et même « officielle ».

6.3.2.2. Théorème

Soit $f$, $g$ et $h$ trois fonctions définies sur un intervalle $I$, voisinage de $\alpha$ (où $\alpha = x_0$ ou $-\infty$ ou $+\infty$).
Si pour tout $x$ de $I$ on a $h(x) \le f(x) \le g(x)$ et si $\lim\limits_{x \to \alpha} g(x) = \lim\limits_{x \to \alpha} h(x) = l$, alors $\lim\limits_{x \to \alpha} f(x) = l$.

Voici le schéma pour le cas $\alpha = +\infty$.

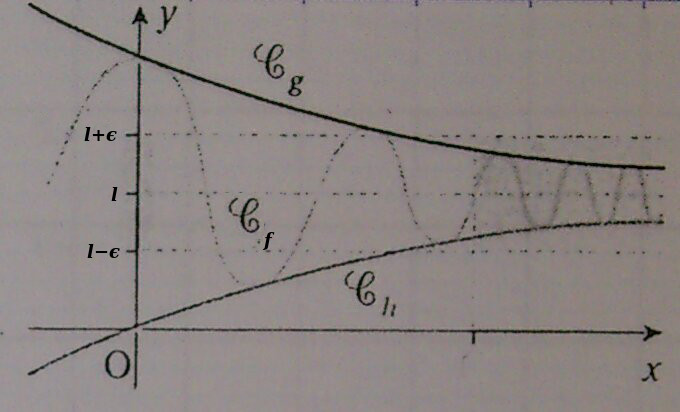
Combien reste-t-il de schémas à faire ?

6.3.2.3. Démonstration

Soit $\epsilon$ un réel strictement positif.

D'après la définition d'une limite finie, il existe un réel $A'$ tel que pour tout $x > A'$, $l - \epsilon < g(x) < l + \epsilon$. Et de même pour $h$ avec un réel noté $A''$.

D'autre part, sur $I$, de la forme $\left] A''', +\infty \right[$, $f$ est comprise entre $g$ et $h$. Donc pour $x > A'''$, $h(x) \le f(x) \le g(x)$.

Finalement, en prenant $A = max(A', A'', A''')$, $A$ convient car pour $x > A$,

$$l - \epsilon \le h(x) \le f(x) \le g(x) \le l + \epsilon$$

(on a gardé une seule des deux inégalités concernant la limite de $g$ et idem pour la limite de $h$).

7. Continuité

7.1. Définitions

7.1.1. Continuité en un point

Si $f$ est définie sur un intervalle $I$ contenant $x_0$, on dit que $f$ est continue en $x_0$ lorsque $\lim\limits_{x \to x_0} f(x) = f(x_0)$.

Schéma (avec loupe) autour de $A(x_0, f(x_0))$.

7.1.2. Continuité sur un ensemble

On dit que $f$ est continue sur $E$ lorsque pour tout $x_0 \in E$, $f$ est continue en $x_0$ (continue en tout point de $E$).

Schéma dans le cas où $E$ est une union d’intervalles.

Si $f$ est continue sur son domaine de définition, alors $C_f$ est en autant de « morceaux » que $D_f$.

7.1.3. Remarques et exemples

• Les limites à droite et à gauche doivent être les mêmes et valoir l'image : $\lim\limits_{\underset{x < x_0}{x \to x_0 }} f(x) = \lim\limits_{\underset{x > x_0}{x \to x_0 }} f(x) = f(x_0)$.
• On admet que les fonctions polynômes, inverse, racine carrée, valeur absolue, trigonométriques ($\sin$, $\cos$, $\tan$, voir le chapitre correspondant), sont continues sur leur ensemble de définition.
• On admet que les sommes, différences, produits, quotients et composées de fonctions continues sont continues sur leur ensemble de définition.
• Dans un tableau de variations, les flèches symbolisent aussi implicitement la continuité.
• Quelques exemples de fonctions non continues sur leur ensemble de définition :
  • la fonction partie entière,
  • la fonction signe,
  • l'indicatrice des rationnels n'est continue nulle part.

7.2. Théorème des valeurs intermédiaires

Ce théorème est admis.

Commencer par cette activité introductive.

7.2.1. Première version

Soit $f$ une fonction définie et continue sur un intervalle $\left[ a; b\right]$. Pour tout réel $\lambda$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ de $\left[ a; b\right]$ tel que $f(c) = \lambda$.

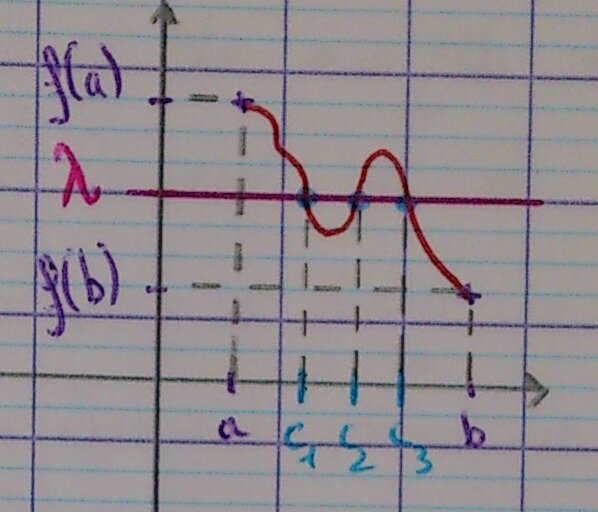
On pourra utiliser parcimonieusement l'acronyme TVI.

7.2.2. Versions étendues

7.2.2.1. Zéros de $f$

Si $f$ est définie et continue sur $\left[ a; b\right]$ et si $f(a)$ et $f(b)$ sont de signes contraires, alors il existe au moins un réel $c$ de $\left[ a; b\right]$ tel que $c$ est un zéro de $f$ (c'est-à-dire $f$ s’annule en $c$, ou même $f(c)=0$).

7.2.2.2. Unicité de l'antécédent

Si en plus des hypothèses de la première version du théorème des valeurs intermédiaires on a aussi l'hypothèse « $f$ est strictement monotone » (que ce soit strictement décroissante ou strictement croissante), alors le réel $c$ est unique.

Cette version est celle qui sera la plus utilisée au baccalauréat.

Exemple : définition de la fonction racine carrée.

1. Montrer qu'il existe un unique réel positif $x$ tel que $x^2 = 2$.
2. Montrer que pour tout réel positif $a$, il existe un unique réel positif $x$ tel que $x^2 = a$. Ce nombre $x$ est la racine carrée de $a$.

Cet exemple parait trivial, mais c'est un principe très utilisé pour définir les fonctions réciproques. On remarque que la courbe représentative de la fonction réciproque est obtenue par symétrie par rapport à la première diagonale.

7.2.2.3. Avec une limite infinie

Si $f$ est définie et continue sur $\left[ a; b \right[$ et si $\lim\limits_{x \to b} f(x) = +\infty$, alors on peut remplacer « $\lambda$ compris entre $f(a)$ et $f(b)$ » par « $\lambda \ge f(a)$

Cette version du TVI :

• peut se décliner avec la borne ouverte en $a$ et/ou avec une limite valant $-\infty$,
• peut se combiner avec la version où l'antécédent est unique,
• peut se démontrer en coupant l'intervalle en $b'$ avec $f(b') \ge \lambda$ en version « unicité » ou non (à savoir faire).

7.2.2.4. Sur un domaine infini

On peut remplacer $\left[ a; b \right]$ par $\left[ a; +\infty \right[$ ou $\left] -\infty; b \right]$ et travailler avec une limite finie ou infinie en $b$ ou en $a$. La démonstration vient encore en coupant notre intervalle en plusieurs morceaux.

7.3. Limite de suites définies par récurrence

7.3.1. Théorème (admis)

Soit $(u)$ est une suite définie par $u_{n+1} = f(u_n)$ pour tout indice $n$. Si :

• $(u)$ converge vers une limite notée $l$,
• $f$ est continue en $l$,

alors $f(l) = l$.

7.3.2. Principe

Ici on utilisera la notation $u_n \to l$ à la place de $\lim\limits_{n \to +\infty} u_n = l$.

Montrons que :

1. $u_{n+1} \to l$
2. $u_{n+1} \to f(l)$

Finalement, par unicité de la limite, on aura $l = f(l)$.

$$ \require{AMSmath} \def\mapright#1{\xrightarrow{#1}} \def\mapdown#1{\Big\downarrow\rlap{\raise2pt{\scriptstyle{#1}}}} \begin{array}{ccc} u_n & \mapright{\text{suivant}} & u_{n+1} \\[3pt] \mapdown{\text{limite}} & & \mapdown{\text{limite}} \\ l & ? & f(l) \end{array}\phantom{h} $$

1) Les suites $(u_n)_{n \in \mathbb N}$, et $(u_{n+1})_{n \in \mathbb N}$ ont la même limite, car si on enlève le premier terme à la suite $(u)$, elle garde la même limite. Autrement dit : comme $u_n \to l$, $u_{n+1} \to l$.

2) D'autre part, puisque :

• $\lim\limits_{n \to +\infty} u_n = l$
• $\lim\limits_{x \to l} f(x) = f(l)$ car $f$ est continue en $l$

on a par (une sorte de) composition $f(u_n) \to f(l)$.

Comme pour tout indice $n$ on a $f(u_n) = u_{n+1}$, on a $u_{n+1} \to f(l)$.

7.3.3. Remarques

• Utilisation fréquente avec le théorème de convergence monotone.

7.3.4. Exemple sur un exercice

Soit $u$ la suite définie par $u_0 = 1$ et pour tout $n \in \mathbb N$, $u_{n+1} = \frac{1}{2} u_n + 1$.

1. Calculer les six premiers termes de $u$ sous forme de fractions, et remarquer que :
   • le numérateur vaut toujours un de moins que le double du dénominateur,
   • le numérateur vaut toujours un de plus que le double du dénominateur moins un.
2. Comment est définie cette suite ? explicitement ou par récurrence ? Définir une fonction $f$ et ré-exprimer la définition de $u$ à l’aide de $f$.
3. $u$ est-elle arithmétique ? géométrique ?
4. Montrer que pour tout entier naturel $n$, $(u_{n+2} - u_{n+1}) = \frac{1}{2}(u_{n+1} - u_n)$. Cette suite illustre donc le paradoxe d’Achille et de la tortue.
5. À l’aide des droites d’équation $y=\frac{1}{2} x + 1$ et $y=x$, construire graphiquement la suite sur l’axe des abscisses. Prendre pour unité une demi-page.
6. Il semble que $u$ converge, vers quelle limite ?
7. Retrouver ce résultat en résolvant $f(l)=l$. Attention à la rédaction, la convergence de $u$ n’a pas été démontrée (voir la remarque suivante) !

La démonstration de la convergence peut se faire par récurrence. Voir la section correspondante d’un prochain chapitre.

Pour la culture : construction graphique des suites définies par récurrence simple.

7.3.5. Remarque

Ce théorême est à appliquer avec prudence : ne pas oublier l’hypothèse « $(u)$ converge ».

Un bon contre-exemple est la suite des puissances de 2. En effet, $f$ est définie par $f(x) = 2x$, et ce n’est pas parce que $0 = 2×0$ que $(u)$ converge vers 0.

D’autre part, l’équation $l = f(l)$ peut avoir plusieurs solutions.