1. Rappels

1.1. Nombre dérivé et tangente à une courbe

1.1.1. Définition

Soit $I$ un intervalle contenant un nombre réel $a$ et $f$ une fonction définie sur $I$. On dit que la fonction $f$ est dérivable en $a$ si la limite du rapport $\frac{f(a+h)-f(a)}{h}$ lorsque $h$ tend vers 0, existe et est égale à un nombre réel $l$.

Ce nombre $l$ est appelé nombre dérivé de la fonction $f$ en $a$ et est noté $f'(a)$.

1.1.1.1. Remarques

1. On peut écrire une définition similaire avec $x$ tel que $h=x-a$, soit $x = a+h$. Quand $h$ tend vers 0, $x$ tend vers $a$.
2. Le quotient de la définition s’appelle le taux d’accroissement.
3. racine (et sinus cardinal ?) ne sont pas dérivables en 0.

1.1.2. Définition

Soit $f$ une fonction définie sur un intervalle $I$, dérivable en $a$, nombre réel appartenant à $I$, et de nombre dérivé $l$ en $a$.

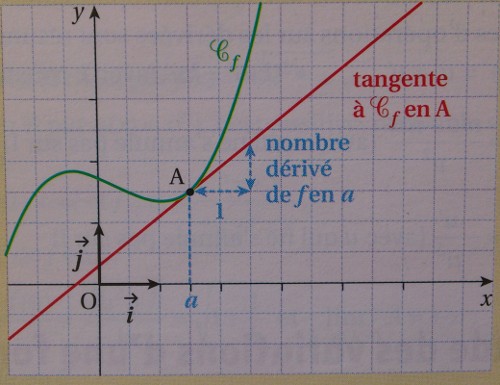
Soit $C_f$ la courbe représentative de la fonction $f$ dans un repère $(O, \vec i, \vec j)$ du plan et $A$ le point de $C_f$ d'abscisse $a$.

La tangente à la courbe $C_f$ au point $A$ est la droite qui passe par $A$ et qui a comme coefficient directeur le nombre dérivé $l$.

On parle de pseudo-tangente. Le taux d’accroissement est le coefficient directeur de cette pseudo-tangente.

Schéma «Cachin» avec quand x tend vers a

1.2. Équation de la tangente en a

$$T_a: y= mx + p~\text{avec}~m=f'(a)$$

$$T_a: y=f'(a) \left( x-a \right) + f(a)$$

Pour comprendre cette formule, remplacer $x$ par $a$.

1.3. Exemple (refaire la hiérarchie de titres!!!)

Cherchons le nombre dérivé de la fonction « carré » en 1.

Démo et schéma.

Idem dans le cas général, où on ne remplace pas $a$ par 1.

On retrouve $f'(a) = 2a$, plus connue sous la forme $f'(x) = 2x$.

2. Fonction dérivée

2.1. Définition

Si $f$ est une fonction définie et dérivable en tout point d’un intervalle $I$, on définit la fonction dérivée de $f$ la fonction :

$$f:I->R x+->f'(x)$$

Cette fonction donne les coefficients directeurs des tangentes à $\mathcal C_f$.

2.2. Exemples

carré, constante, puiss n, racine, inverse, inverse puissance (avec diagramme à flèches), affine, cos, sin

2.3. Opérations

2.3.1. Connues

somme, diff, produit, prod pas cste, somme par cste, quotient

2.3.2. Composition

2.3.2.1. Définition

On notera $f(g(x)) = f \circle g(x)$ (composée de g par f)

Diagramme à flèches.

Quelques exemples et exercices simples ici. Un déménagement s’impose si ce chapitre passe dans le chapitre zéro.

Nombre dérivé, puis formule point-free, puis avec x

2.3.2.2. Dérivée d’une composée

quotient, puis dénominateur avant !

Quand x->a…

2.3.2.3. Cas particuliers

g(x) = ax+b (recopie du coeff)

f(x) = x^{2 (f(z) = z}2 et f'(z)=2z)

f(x) = x^n

f(x) = \sqrt x

f(x) = 1/x

Attention, les formules sont parfois à utiliser avec des $u$ ou $v$, voire en inversant le rôle de $f$ et de $g$.

Tableaux

• si $f(x) = sin(u(x))$ alors $f'(x)=...$
• si $f(x) = cos(u(x))$ alors $f'(x)=...$
• si $f(x) = exp(u(x))$ alors $f'(x)=...$