Primitives
1. Définition
Soit $f$ une fonction définie sur un intervalle $I$.
Une fonction $F$ définie sur $I$ est une primitive de $f$ sur $I$ si $F$ est
dérivable sur $I$ et si sa dérivée est $f$, c’est-à-dire :
- pour tout $x$ de $I$ on a $F'(x) = f(x)$, ou même
- $F' = f$.
1.1. Exemples
Pourrez-vous trouver quelques exemples ?
- $f(x) = 2x$ et $F(x) = x^2$,
- $f(x) = 2x$ et $F(x) = x^2 + 3$,
- $f(x) = \frac{1}{x^2}$ et $F(x) = -\frac{1}{x}$,
- …
1.2. Remarques
C’est le processus inverse de la dérivation (qu’il faut donc maîtriser).
$$F \longrightarrow f \longrightarrow f' \longrightarrow f'' \longrightarrow …$$
Nous allons voir tout de suite pourquoi nous parlons d’une primitive et non de la primitive.
2. Propriétés
2.1. Infinité de primitives
Sur un intervalle $I$, si une fonction $F$ est une primitive de la fonction $f$, alors toute fonction $G$ définie sur $I$ par $G(x) = F(x) + k$ où $k$ est un réel est également une primitive de $f$ sur $I$.
Démonstration laissée en exercice.
Remarque : Comme il y a une infinité de $k$ possibles, $f$ a donc au moins une infinité de primitives.
2.2. Lien entre les primitives
Sur un intervalle $I$, si $F$ et $G$ sont les primitives d’une même fonction $f$, alors il existe un nombre réel $k$ tel que pour tout réel $x$ de $I$ on a : $$G(x) = F(x) + k$$
Démonstration laissée en exercice (il suffit d’étudier la différence des deux fonctions).
Remarque : Les primitives d’une fonction forment donc une famille de fonctions dont on peut dire :
- deux primitives diffèrent d’une constante,
- une fois une primitive trouvée, nous avons facilement accès à toutes les autres.
2.3. Primitive respectant une condition initiale
Soit $f$ une fonction définie sur un intervalle $I$. Si $f$ admet une primitive $F$ sur $I$, alors pour tout couple $\left(x_0; y_0\right)$ avec $x_0 \in I$ et $y_0 \in \mathbb R$ il existe une unique primitive $F_0$ telle que $F_0 \left( x_0 \right) = y_0$.
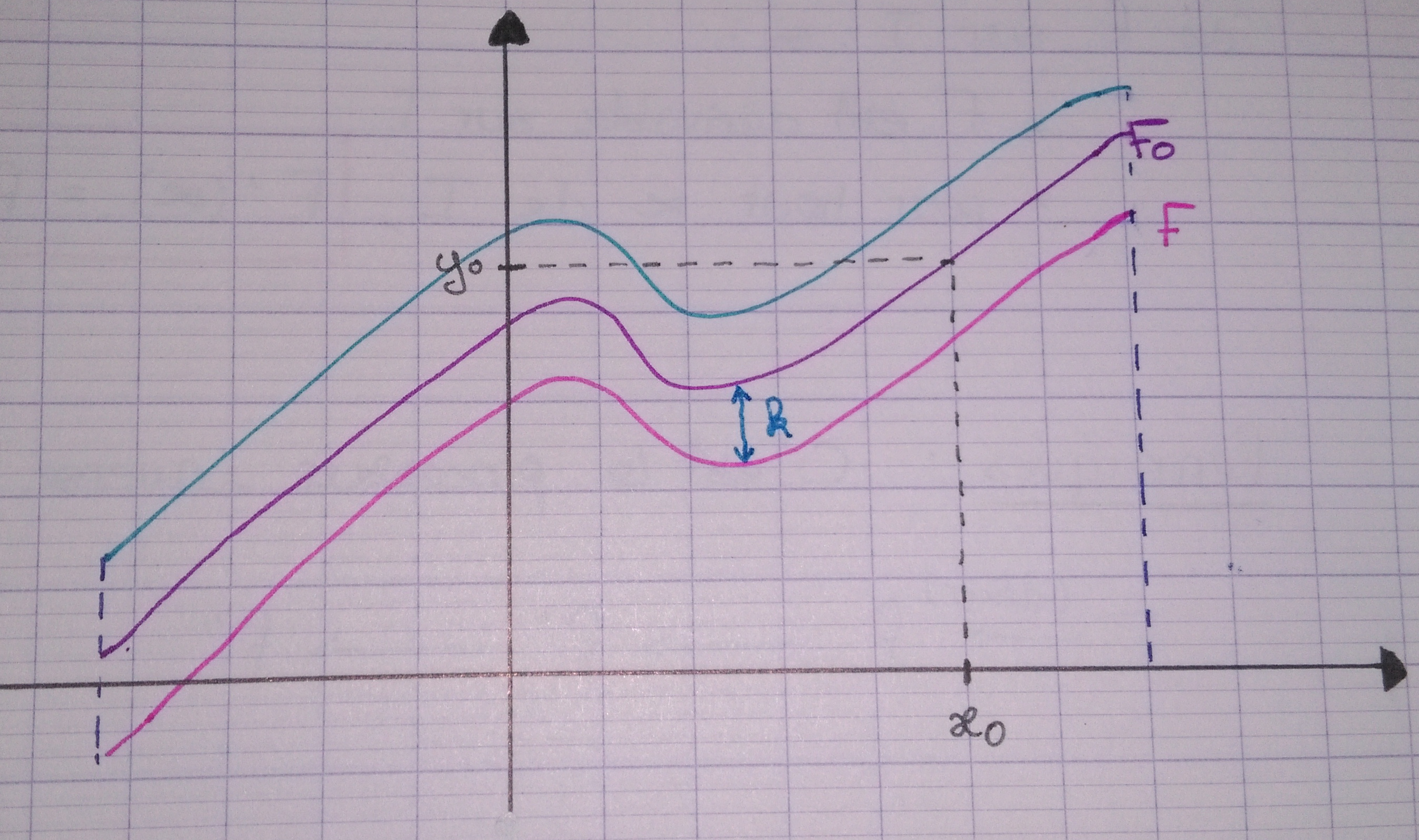
C’est un exercice très classique que de trouver le $k$ séparant $G$ de $F$ connaissant le couple $\left(x_0; y_0 \right)$.
Exercice modèle
On définit $f$ par $f(x) = x$. Trouver la primitive de $f$ qui vaut 2 en 1.
Exemple de rédaction
On note $F(x) = \frac{1}{2} x^2 + K$. $K$ est telle que $F(1)=2$, et donc $\frac{1}{2} 1^2 + K = 2$, c’est-à-dire $K = 2 - \frac{1}{2} = \frac{3}{2}$.
2.4. Lien avec l’intégration
2.4.1. Calcul d’intégrales
2.4.1.1. Théorème
Soit $f$ une fonction définie, continue et positive sur un intervalle $[a;b]$.
Si $F$ est une primitive de $f$ sur $[a;b]$, alors on a :
$$\int_a^b f(x)~dx = F(b) - F(a)$$
Notation : Afin de faciliter la présentation des calculs, on note :
$$ F(b) - F(a) = \left[ F(x) \right]_a^b $$
On prononcera : « F de $x$ entre $a$ et $b$ ».
Remarque : Comme deux primitives ne diffèrent que d’une constante, ce calcul ne dépend pas de la primitive choisie. En effet, pour une autre primitive $G$, comme il existe un $k$ tel que pour tout $x \in [a;b]$ on a $G(x) = F(x) + k$,
$$G(b) - G(a) = \left( F(b) + k \right) - \left( F(a) + k \right) = F(b) - F(a)$$
2.4.1.2. Démonstration
D’après un résultat d’une section du chapitre sur l’intégration, on sait que la fonction $G$ définie sur $[a;b]$ par $G(x) = \int_a^x f(t)~dt$ est une primitive de $f$ sur $[a;b]$.
D’après une section de ce chapitre, on sait qu’il existe un réel $k$ tel que pour tout $x$ de $[a;b]$ on a : $G(x) = F(x) + k$.
$G$ s’annullant en $a$, on a $k = -F(a)$. Finalement, on a pour tout $x$ :
$$\int_a^x f(t)~dt = F(x) - F(a)$$
et en prenant $x = b$ :
$$\int_a^b f(t)~dt = F(b) - F(a)$$
2.4.1.3. Exemple
Calculer $\int_1^3 (4x+2)~dx$.
2.4.2. Existence de primitives
2.4.2.1. Théorème
Toute fonction continue sur un intervalle admet des primitives sur cet intervalle.
2.4.2.2. Démonstration
Soit $f$ une fonction continue sur un intervalle $I$.
La démonstration se fait en admettant :
- que $I$ est un intervalle de la forme $[a;b]$,
- que $f$ admet un minimum sur $I$.
Remarque : il est possible de prouver qu’une fonction continue admet un minimum $m$ sur un intervalle de la forme $[a;b]$.
Voir la démonstration page 244.
2.4.2.3. De l’existence à l’expression
Même si l’on sait qu’une primitive existe c’est une autre affaire que de l’exprimer.
Voir cet article.
3. Tableaux de primitives
3.1. Primitives des fonctions puissance
À partir du tableau des dérivées des fonctions puissance, où $n \neq 0$ et $n' = -n$ :
| n | $f(x) = x^n = \frac{1}{x^{n'}}$ | $f'(x) = nx^{n-1} = -n' x^{-n'-1} = -n' \frac{1}{x^{n'+1}}$ |
|---|---|---|
| … | … | … |
| 3 | $x^3$ | $3x^2$ |
| 2 | $x^2$ | $2x^1 = 2x$ |
| 1 | $x^1 = x$ | $x^0 = 1$ |
| -1 | $x^{-1} = \frac{1}{x}$ | $-x^{-2} = -\frac{1}{x^2}$ |
| -2 | $x^{-2} = \frac{1}{x^2}$ | $-2x^{-3} = -\frac{2}{x^3}$ |
| -3 | $x^{-3} = \frac{1}{x^3}$ | $-3x^{-4} = -\frac{3}{x^4}$ |
| … | … | … |
on en déduit celui-ci, où $n \neq -1$ :
| n | $f(x) = x^n = \frac{1}{x^{n'}}$ | $F(x) =~?$ |
|---|---|---|
| … | … | … |
| 3 | $x^3$ | $\frac{1}{4} x^4$ |
| 2 | $x^2$ | $\frac{1}{3} x^3$ |
| 1 | $x^1 = x$ | $\frac{1}{2} x^2$ |
| 0 | $x^0 = 1$ | $x$ |
| -2 | $x^{-2} = \frac{1}{x^2}$ | $-x^{-1} = -\frac{1}{x}$ |
| -3 | $x^{-3} = \frac{1}{x^3}$ | $-\frac{1}{2} x^{-2} = -\frac{1}{2} \frac{1}{x^2}$ |
| … | … | … |
La formule est donc :
si $f(x) = x^n$ alors une primitive de $f$ est $F$ avec $F(x) = \frac{x^{n+1}}{n+1}$.
si $f(x) = \frac{1}{x^n}$ alors une primitive de $f$ est $F$ avec $F(x) = -\frac{1}{n-1} \frac{1}{x^{n-1}}$.
Exercice : Devinettes en groupe.
3.1.1. Tableaux
3.1.2. Primitive manquante
| n | $f(x) = x^n$ | $f'(x) = nx^{n-1}$ | $f'(x) = kx^{n'}$ où $n'=…$ |
|---|---|---|---|
| … | … | … | … |
| 3 | $x^3$ | $3x^2$ | 2 |
| 2 | $x^2$ | $2x^1 = 2x$ | 1 |
| 1 | $x^1 = x$ | $x^0 = 1$ | 0 |
| 0 | $x^0 = 1$ | $0$ | pas de $n'$ |
| ? | ? | $x^{-1} = \frac{1}{x}$ | -1 |
| -1 | $x^{-1} = \frac{1}{x}$ | $-x^{-2} = -\frac{1}{x^2}$ | -2 |
| -2 | $x^{-2} = \frac{1}{x^2}$ | $-2x^{-3} = -\frac{2}{x^3}$ | -3 |
| -3 | $x^{-3} = \frac{1}{x^3}$ | $-3x^{-4} = -\frac{3}{x^4}$ | -4 |
| … | … | … | … |
Lorsque l’on dérive les $x^n$ pour $n \in \mathbb Z$, on s’aperçoit qu’il manque quelque chose à l’arrivée.
La fonction dont la dérivée est la fonction inverse n’est pas une fonction puissance.
3.2. Primitives des autres fonctions usuelles
Voir livre page 243 n°2.
3.3. Primitives et opérations sur les fonctions
3.3.1. Généralités
Rappels :
- La dérivée d’une somme est la somme des dérivées.
- La dérivée d’une différence est la différence des dérivées.
- La dérivée d’un produit par une constante est le produit par cette constante de la dérivée.
Mais :
- La dérivée d’un produit n’est pas le produit des dérivées.
- La dérivée d’un quotient n’est pas le quotient des dérivées.
- La dérivée d’une composée n’est pas la composée des dérivées.
On obtient des propriétés similaires pour les primitives.
Voir livre page 243.
3.3.2. Composition avec fonctions de référence
Rappels :
- La dérivée de $u^n$ est $u'u^{n-1}$.
- La dérivée de $\frac{1}{u^n}$ est $u'u^{-n-1}$.
- …
Donc :
- Une primitive de $u'u^n$ est $\frac{1}{n+1}u^{n+1}$.
- Une primitive de $\frac{u'}{u^n}$ est $-\frac{1}{(n-1)u^{n-1}}$.
- …
3.3.3. Composition avec une fonction affine
Une primitive de $f$ où $f(x) = e ^ {ax + b}$ est $F$ où $F(x) = \frac{1}{a} e ^ {ax + b}$.
Une primitive de $f$ où $f(x) = \ln (ax + b)$ est $F$ où $F(x) = \frac{1}{a} \ln (ax + b)$.
3.4. Quelques trucs
3.4.1. Primitive de la fonction racine
Penser à dériver $u$ où $u(x) = x \sqrt x$.
3.4.2. Primitive de la fonction logarithme
Penser à dériver $u$ où $u(x) = x \ln x$.
