Complexes et géométrie
Ce chapître requiert celui de trigonométrie :
- lignes trigonométriques,
- parité,
- $\cos$ et $\sin$ d’une somme,
- …
Table des matières :
1. Activité rapide d’introduction
Soit $O$ le point d’affixe $0$, $A$ le point d’affixe $1$ et $B$ le point d’affixe $1+i\sqrt 3$.
Calculer $OA$, $OB$ et une mesure de l’angle $\widehat{AOB}$.
2. Affixe et image
Soit un repère orthonormé direct $\left( 0; \vec u; \vec v \right)$.
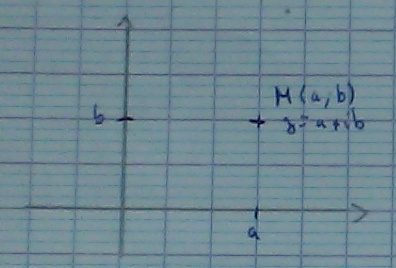
| $\mathbb C$ | le plan |
|---|---|
| $z = a + ib$ | $M(a;b)$ ou $M(z)$ |
| $a$ : partie réelle de $z$ | $a$ : abscisse de $M$ |
| $b$ : partie imaginaire de $z$ | $b$ : ordonnée de $M$ |
| $z$ est l’affixe de $M$ | $M$ est l’image de $z$ |
| $\mathbb R$ | axe des abscisses |
| $i \mathbb R$ | axe des ordonnées |
On peut aussi noter $z_M$ l’affixe de $M$.
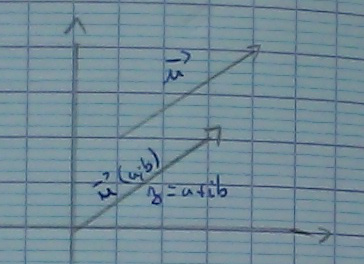
On parle aussi de l’affixe d’un vecteur. On a :
- Si $A$ et $B$ sont deux points du plan, $z_{\vec {AB}} = z_B - z_A$.
En effet : $$\begin{aligned} z_{\vec {AB}} &= (x_B - x_A) + i(y_B - y_A) \\\\ &= x_B + i y_B - x_A - i y_A \\\\ &= x_B + i y_B - (x_A + i y_A) \end{aligned}$$ - Si $\vec w_1$ et $\vec w_2$ sont deux vecteurs,
$z_{\vec w_1 + \vec w_2} = z_{\vec w_1} + z_{\vec w_2}$.
(calcul) - Si $k$ est un nombre réel, $z_{k \vec w} = k z_{\vec w}$.
(calcul)
3. Module d'un nombre complexe
3.1. Définition
Soit $z$ un nombre complexe d'écriture algébrique $z = a + ib$. Le module de $z$ est noté $\left| z \right|$ et est défini par $\left| z \right| = \sqrt{a^2 + b^2}$.
3.2. Exemples et remarques
- Dans un repère orthonormé, si A est le point de coordonnées (a;b), alors $\left| z \right| = OA$.
- $\left| 3 - 5i \right| = …$
- Il est parfois plus présentable de calculer le carré du module avant de calculer le module lui-même (comme pour le théorème de Pythagore).
- Si $z$ est réel, $$\begin{aligned} \left| z \right| &= \left| a + 0i\right| \\\\ &= \sqrt {a^2 + 0^2} \\\\ &= \sqrt {a^2} \\\\ &= \underbrace{\left| a \right|}_{\text{val. absolue}} \end{aligned}$$ On peut dire que le module étend la notion de valeur absolue (ce qui est cohérent avec la notation).
- Si $z$ est imaginaire pur, $\left| z \right| = \left| 0 + ib \right|
= \sqrt {b^2} = \left| b \right|$.
(On rappelle que la partie imaginaire est réelle).
3.3. Propriétés du module
Pour tous complexes $z$ et $z'$, on a les propriétés ou égalités suivantes :
- $\left| z \right|$ est un réel positif, d’où de plus :
- $\left| \left| z \right| \right| = \left| z \right|$ (le module est idempotent, comme une projection)
- $\overline {\left| z \right|} = \left| z \right|$
- Avec zéro, opposé et conjugué :
- Si $z$ est nul, $\left| z \right| = 0$.
- Réciproquement, si $\left| z \right| = 0$, alors $z = 0$.
- $\left| -z \right| = \left| z \right|$
- $\left| \overline z \right| = \left| z \right|$
- $z \overline z = \left| z \right| ^2$
- Avec le produit :
- $\left| z×z' \right| = \left| z \right| × \left| z' \right|$
- si $k \in \mathbb R$, $\left| k×z \right| =
\left| k \right| × \left| z \right|$,
où les premières barres peuvent être vues comme la valeur absolue, et
les autres comme le module.
Exemple : $\left| -4 z \right| = 4 \left| z \right|$ - pour $n \in \mathbb N$, $\left| z^n \right| = \left| z \right|^n$
- Avec le quotient :
- si $z \ne 0$, $\left| \frac{1}{z} \right| = \frac{1}{\left| z \right|}$
- si $z' \ne 0$, $\left| \frac{z}{z'} \right| = \frac{\left| z \right|}{\left| z' \right|}$
- si $z \ne 0$, $\left| \frac{z}{ \left| z \right|} \right| = 1$
- si $z \ne 0$, $\left| \frac{z}{\overline z} \right| = 1$ (anecdotique)
- Avec la somme :
- $\left| z+z' \right| \le \left| z \right| + \left| z' \right|$ (inégalité triangulaire)
- L’égalité est un cas très particulier, vu dans un prochain chapitre.
- Avec les parties réelles et imaginaires :
- $\left| \mathcal{Re} (z) \right| \le \left| z \right|$
- $\left| \mathcal{Im} (z) \right| \le \left| z \right|$
Il est intéressant de traduire chacune de ces égalités par une phrase en français.
Démonstrations laissées en exercice, avec indications :
- Directement d’après la définition (la racine carrée de la somme de carrés de
nombres réels est un réel positif ou nul).
- Le module d'un réel positif ou nul est ce même réel.
- Le conjugué d'un réel est ce même réel.
- Avec zéro, opposé et conjugué :
- Si $z$ est nul, $\left| z \right| = \left| 0 + 0i \right| = \sqrt {0^2 + 0^2} = \sqrt 0 = 0$.
- En posant $z=a+ib$, on a $\sqrt {a^2 + b^2} = 0$.
Comme seul 0 annule la fonction racine carrée, on a $a^2 + b^2 = 0$.
Ces carrés étant positifs ou nuls, la seule façon d'annuler la somme est qu'ils soient nuls tous les deux. On a donc $a^2 = 0$ et $b^2 = 0$. Comme seul 0 annule la fonction carré, on a $a=0$ et $b=0$, c'est-à-dire $z = 0$. - Directement d’après la définition, car un réel a le même carré que son opposé.
- Idem.
- Vu dans les propriétés du conjugué.
- Avec le produit :
- Utiliser la forme algébrique ou $z \overline z$.
- Cas particulier de la propriété précédente, $\left| k \right|$ est en fait la valeur absolue de $k$.
- Par récurrence.
- Avec le quotient :
- Utiliser la forme algébrique (calcul similaire à un calcul fait pour le conjugué de l'inverse).
- Découle des propriétés précédentes (le quotient est le produit par l’inverse).
- On peut utiliser une propriété précédente en posant $k = \frac{1}{\left| z \right|}$ si on utilise le produit ou $k = \left| z \right|$ si on utilise le quotient.
- Découle des propriétés précédentes.
- Avec la somme :
- Calculer les carrés des modules en utilisant les formes algébriques.
On peut aussi raisonner géométriquement. - À explorer soi-même, excellent travail de recherche !
- Calculer les carrés des modules en utilisant les formes algébriques.
- On peut utiliser la forme algébrique de $z$ ou raisonner géométriquement.
4. Argument
4.1. Définition
Soit $z$ un nombre complexe non nul, et $M$ son image dans un repère orthonormé
direct $\left( 0; \vec u; \vec v \right)$. Un argument de $z$ est une mesure
en radians de l’angle orienté $\left( \vec u; \vec {OM} \right)$.
On le note $\arg (z)$.

4.2. Remarques et premiers exemples
- Un argument est défini à $2 \pi$ près. Un nombre complexe a donc une infinité d’arguments.
- $\arg (1) = …$
- $\arg (2) = …$
- $\arg (i) = …$
- $\arg (2i) = …$
- $\arg (-1) = …$
- $\arg (-i) = …$
- $\arg (1 + i \sqrt 3) = …$
- $\arg (\sqrt 3 + i) = …$
L’image $M$ d’un complexe $z$ peut être repérée grâce à :
- $\mathcal {Re}(z)$ et $\mathcal {Im}(z)$ (abscisse et ordonnée en coordonnées cartésiennes) ;
- $\left|z\right|$ et $arg z$ (distance à l’origine et angle en coordonnées polaires).
5. Forme trigonométrique
5.1. Projection sur le cercle trigonométrique
5.2. Propriété fondamentale de l’argument
Pour tout nombre réel $\theta$, on pose $f(\theta) = \cos \theta + i \sin \theta$.
La fonction $f$ est donc définie sur $\mathbb R$ et prend ses valeurs dans $\mathbb C$.
$f(\theta)$ est l’affixe du point du cercle trigonométrique de coordonnées $(cos(\theta);sin(\theta))$. (schéma)
Soit $\theta$ et $\theta'$ deux nombres réel. On a :
$$\begin{aligned} f(\theta)×f(\theta') &= \left( \cos \theta + i \sin \theta \right) × \left( \cos \theta' + i \sin \theta' \right) &(1) \\\\ &= \cos \theta × \cos \theta' + \cos \theta × i \sin \theta' + i \sin \theta × \cos \theta' + i \sin \theta × i \sin \theta' &(2) \\\\ &= \left( \cos \theta \cos \theta' - \sin \theta \sin \theta' \right) + i \left( \cos \theta \sin \theta' + \sin \theta \cos \theta' \right) &(3) \\\\ &= \cos (\theta + \theta') + i \sin (\theta + \theta') &(4) \\\\ &= f(\theta + \theta') &(5) \end{aligned}$$
- Définition de $f$.
- Développement (pour les débutants).
- Distinction partie réelle et imaginaire.
- Cosinus et sinus d’une somme.
- Définition de $f$.
Tout se passe comme si l’argument d’un produit était la somme des arguments.
5.3. Propriétés de l’argument
On note que les éléments neutres sont respectés puisque $f(0) = 1$, et on pourrait montrer de même que :
$$\begin{aligned} \frac{f(\theta)}{f(\theta')} &= f(\theta - \theta') \\\\ \frac{1}{f(\theta')} &= f(- \theta') \\\\ f(\theta)^2 &= f(2 \theta) \end{aligned}$$
D’où les propriétés suivantes :
$$\begin{aligned} arg(z z') &= arg(z) + arg(z') & \left[ 2\pi \right] \\\\ arg(\frac{z}{z'}) &= arg(z) - arg(z') & \left[ 2\pi \right] \\\\ arg(\frac{1}{z}) &= -arg(z) & \left[ 2\pi \right] \\\\ arg(z^2) &= 2 arg(z) & \left[ 2\pi \right] \\\\ arg(z^n) &= n arg(z) & \left[ 2\pi \right] \\\\ \end{aligned}$$
Avec des dénominateurs non nuls et $n$ un entier.
De plus, si $k>0$ alors $arg(kz) = arg(z) \left[ 2\pi \right]$, et si $k<0$ alors $arg(kz) = arg(z) + \pi \left[ 2\pi \right]$.
5.4. Avec des vecteurs
Il est intéressant de regarder le sens de la deuxième égalité si on considère que $z$ et $z'$ sont les affixes des vecteurs, disons $\vec n$ et $\vec m$. On a, à $2\pi$ près :
$$\begin{aligned} arg(\frac{z_{\vec n}}{z_{\vec m}}) &= arg(z_{\vec n}) - arg(z_{\vec m}) \\\\ &= \left( \vec u; \vec n \right) - \left( \vec u; \vec m \right) \\\\ &= \left( \vec u; \vec n \right) + \left( \vec m; \vec u \right) \\\\ &= \left( \vec m; \vec u \right) + \left( \vec u; \vec n \right) \\\\ &= \left( \vec m ; \vec n \right) \\\\ \end{aligned}$$
Le principe du « la fin moins le début » se traduit par « la fin divisée par le début ».
6. Forme exponentielle
6.1. Définition
6.2. Exemples
$iz = r e^{i(\theta + \frac{\pi}{2})}$
$-z = r e^{i(\theta + \pi)}$
6.3. Exercice type
Sachant que $\frac{1}{3} - \frac{1}{4} = \frac{1}{12}$, écrire de deux façons le nombre $e ^ {i \frac{\pi}{12}}$. En déduire les valeurs exactes de $\cos \frac{\pi}{12}$ et $\sin \frac{\pi}{12}$.
7. Liens avec la géométrie
Soit $M$ le point d’affixe $z$.
Pour visualiser l’égalité $Z=\frac{z - z_A}{z_B - z_A} = r e^{i\theta}$, nous allons fixer $z_A = 0$ et $z_B = 1$ et étudier les cas suivants :
- $z=0$
- $z=1$
- $z=2$
- $z=3$
- $z=\frac{1}{2}$
- $z=i$
- $z=1+i$
- $z=2+2i$
- $z=-1+i$
Calculer $Z$ puis faire une figure dans chaque cas.
Conclure par une figure qui décrit le cas général.
