Démonstration
Cette page montre ce dont est capable le générateur de ce site (voir cet article). Attention, pour afficher correctement les formules mathématiques, certains schémas, certaines animations, colorer le code source… il faut non seulement activer Javascript sur votre navigateur, mais aussi être connecté à Internet.
La source de ce document peut-être obtenue en remplaçant .html par .txt
dans la barre d’adresse de votre navigateur ou bien en cliquant sur le lien
« source » tout en bas à droite de la page (comme toutes les pages
de ce site d’ailleurs).
Voici une table des matières de cette page (faite à la main car la table des matières générée automatiquement que vous trouverez plus loin est presque trop complète) :
- Markdown
- Extensions à Python-Markdown
- HTML pur
- Mathjax
- Ditaa
- JSX Graph
- highlight.js
- Contenu escamotable
- Diaporamas
- Online Python Tutor
- Processing.js
- Timeline
- Pre3d
- Delicious
1. Markdown
La conversion Markdown -> HTML est faite par Python-Markdown. Cet outil respecte la syntaxe officielle Markdown, que je vais rapidement expliquer ici en français.
Certaines extensions peuvent être activées afin d’étendre cette syntaxe de base.
1.1. Paragraphes et sauts de ligne
Les paragraphes sont séparés par toute ligne qui a l’air vide (soit effectivement vide, soit contenant uniquement des espaces ou tabulations).
Passer à la ligne dans le code source de la page ne fera pas passer à la ligne
une fois la page rendue.
Pour passer à la ligne sans changer de paragraphe (c’est ce qu’il vient de se
passer), il faut terminer la ligne par deux espaces, puis aller à la ligne.
1.2. Caractère d’échappement
Faire précéder un caractère spécial par \ désactive le formatage qu’il
devait occasionner.
Voir cet
article Wikipedia
pour un point de vue général sur le concept.
1.3. Titres
Il faut faire précéder le titre par des dièses #. Plus il y en a,
moins le titre est important.
Les deux plus hauts niveaux de titres peuvent aussi être obtenus
en soulignant avec des = ou des - (c’est ce que je fais le
plus souvent). Les sous-sous-sections sont donc marquées par ###.
1.4. Citations
Je cite :
La citation du moment était :
L’ombre du zèbre n’est pas rayée.
1.5. Listes
- Listes (et sous-listes) non numérotées
- Listes numérotées (la numérotation dans le code source n’a aucun effet)
- Éléments longs (dépassant une ligne)
Liste numérotée :
- Tondre la pelouse
- Vérifier s’il n’y a rien qui traîne
- Vérifier le carburant
- Tailler le pêcher
- Se documenter sur Internet
- Retrouver le sécateur
Liste non numérotée :
- Légumes
- Carottes
- Poireaux
- Fruits
- Clémentines
- Bananes
Liste à paragraphes et éléments longs (numérotée pour bien faire apparaître que c’est la même liste) :
-
Premier élément.
-
Cet élément est très long. Tellement long qu’il dépasse une ligne. Du coup, il faut continuer de l’écrire sur la ligne suivante.
Je peux même continuer le deuxième élément ici.
Il y a encore d’autres
subtilités mais je
ne détaille pas tout ici. Mentionnons juste que si le . est échappé avec un
\, la ligne n’est pas transformée en liste.
- Quelle année !
2003. Quelle année !
1.6. Code source
Voir la section highlight.js.
1.7. Traits de séparation horizontaux
Au moins trois tirets (ou trois astérisques, mais je préfère les tirets).
1.8. Liens
Je n’utilise quasiment pas les liens spécifiés en référence à la fin du fichier source. Je préfère mettre l’adresse cible près du texte qui constitue le lien.
Voici un lien qui pointe vers une page inexistante.
Voici un lien qui pointe vers une page inexistante, mais qui a une bulle.
Sinon, il est possible de créer un lien vers une adresse sans devoir lui donner
un texte autre que l’adresse elle-même :
http://profgra.org/lycee/demo.html#liens.
Cela fonctionne aussi avec les adresse email : profgra.org@gmail.com.
1.9. Emphase
Les astérisques simples et doubles (ou underscores, mais je préfère les
astérisques) produisent respectivement des balises <em></em> ou
<strong></strong>, qui sont respectivement rendus sur les pages par de
l’italique et du gras.
Il est aussi possible d’utiliser les astérisques à l’intérieur d’un mot.
Comme d’habitude, échapper les astérisque *casse la mise en forme*.
1.10. Code en ligne
Voici du code inline grâce au caractère ` (backtick).
Il suffit de taper le code `entre backticks`.
Cela permet d’avoir une police à chasse fixe. Je m’en sers aussi pour symboliser les touches du clavier ou pour d’autres effets.
1.11. Images
La syntaxe n’est pas très souple, mais permet d’insérer des bulles facilement. Si l’on veut ajuster la taille, il faut taper l’insertion de l’image en html pur soi-même :
<img src="chemin" alt="description" width="largeur" height="hauteur" />.


De même que pour les liens, je ne me sers pas de la spécification du chemin des images par référence, avec le chemin de l’image à la fin du fichier source.
2. Extensions
2.1. TOC
Elle est déclenchée grâce à [TOC], mais nécessite d’activer l’extension
toc, incluse dans Python-Markdown.
Attention, sur ce site, si vous tentez d’imprimer une page, les tables des matières générées ainsi n’apparaitront pas.
- Markdown
- Extensions
- HTML pur
- Mathjax
- Opérations
- Égalités, inégalités
- Ensembles de nombres
- Flèches
- Lettres grecques
- Lettres cursives
- Géométrie
- Fonctions de référence
- Ensembles et probas
- Mise en forme dans les formules
- Parenthèses, crochets, accolades
- Au-dessus et en-dessous
- Systèmes
- Poursuite d’égalités
- Limites
- Intégrales
- Logique
- Vecteurs
- Matrices
- Diagrammes
- Autres
- Ditaa
- JSXGraph
- highlight.js
- Contenu escamotable
- Diaporamas
- Online Python Tutor
- Processing.js
- Timeline
- Pre3d
- Delicious
2.2. Tables
Cette extension est incluse dans Python-Markdown et permet de faire des tableaux simples :
| (titre 1) | (titre 2) | (titre 3) |
|---|---|---|
| L’alignement | et | MD |
| des colonnes est possible, | la syntaxe | aussi, voire les $maths$. |
Attention à de pas laisser 4 espaces devant le premier titre.
Ces tableaux sont par exemple utilisés pour présenter les articles sur la page d’accueil ou sur le blog.
2.3. Superscript
C’est au XVIème siècle que Cardan publia une méthode pour résoudre des équations du troisième degré.
2.4. Mathjax, Ditaa
Extensions inspirées de celle-ci, qui empêchent la conversion Markdown du code LaTeX/MathJax, et du code Ditaa. Voir plus loin pour les exemples Mathjax et les exemples Ditaa.
2.5. Prefixedheaders
Extension « maison » qui se charge de la numérotation automatique des titres (comme 2.5.).
2.6. Stop
Extension « maison », qui me permet de cacher la fin d’un cours que j’ai déjà préparé, mais que je ne veux pas montrer tout de suite.
3. HTML pur
Le HTML est laissé intact par Markdown. C’est la méthode de la dernière chance.
Cela permet aussi d’insérer des commentaires dans le code source Markdown, qui apparaîtront dans le code source HTML, sans qu’ils n’apparaissent une fois la page rendue.
3.1. Taille
3.2. Entités
♭ (♭), ♮ (), ♯ (♯)
3.3. SVG
3.3.1. En ligne
Code :
<?xml version="1.0" encoding="UTF-8"?>
<svg xmlns:svg="http://www.w3.org/2000/svg" xmlns="http://www.w3.org/2000/svg"
width="150" height="100">
<g>
<circle cx="75" cy="50" r="40"
style="fill:#f00; stroke:#000; stroke-width:6;" />
</g>
</svg>
3.3.2. Dans un fichier
Code :
<img alt="diagramme de l’union" src="img/operations_ensembles/venn0111.svg" />
3.4. Éditeurs
4. Mathjax
4.1. Opérations
4.1.1. Usuelles
+-/*±−÷×
4.1.2. Racines
$\sqrt{2}$ $\sqrt[n]{2}$
4.1.3. Fractions
$\frac{2}{3}$ est rationnel, $\sqrt{2}$ ne l’est pas.
$$ \begin{aligned} u_n &= a_p n^p + a_{p-1} n^{p-1} + a_{p-2} n^{p-2} + ... + a_2 n^2 + a_1 n + a_0 \\\\ &= a_p n^p \left( 1 + \frac{a_{p-1} n^{p-1}}{a_p n^p} + \frac{a_{p-2} n^{p-2}}{a_p n^p} + ... + \frac{a_2 n^2}{a_p n^p} + \frac{a_1 n}{a_p n^p} + \frac{a_0}{a_p n^p} \right) \\\\ &= a_p n^p \left( 1 + \frac{a_{p-1}}{a_p} \frac{1}{n} + \frac{a_{p-2}}{a_p} \frac{1}{n^2} + ... + \frac{a_2}{a_p} \frac{1}{n^{p-2}} + \frac{a_1}{a_p} \frac{1}{n^{p-1}} + \frac{a_0}{a_p} \frac{1}{n^p} \right) \\\\ \end{aligned} $$
Fractions continues :
$$\underset{j=1}{\overset{\infty}{\LARGE\mathrm K}}\frac{a_j}{b_j} =\cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\ddots}}}$$
4.1.4. Divers
$f \circ g$
4.1.5. Indices, puissances
$(1000)_{16}$
$2^{10} = 1024$
4.2. Égalités, inégalités
$$ n \ge 0 $$ $$ 0 \le n $$ $$ x \neq 1 $$ $$e^{\lambda t} - 1 \sim \lambda t$$ $$ x \equiv y [n] $$ $$ x \approx 1,96 $$
4.3. Ensembles de nombres
$$\mathbb N \subset \mathbb Z\ \subset \mathbb D \subset \mathbb Q \subset \mathbb R \subset \mathbb C \subset \mathbb H \subset \mathbb O$$
$\supset$ $\not\subset$
$\emptyset$ (\varnothing et \O ne fonctionnent pas)
$$ \begin{aligned} S &= \left\{ \frac{\pi}{4} + 2 k \pi; k \in \mathbb Z \right\} \cup \left\{ \frac{3\pi}{4} + 2 k' \pi; k' \in \mathbb Z \right\} \\\\ &= \left\{ \frac{\pi}{4} + k \pi; k \in \mathbb Z \right\} \\\\ \end{aligned} $$
4.4. Flèches
$$u_n \to l$$
$$A \overset{g}{\longrightarrow} B \overset{f}{\longrightarrow} \Gamma$$ $$\alpha \overset{g}{\longmapsto} \beta \overset{f}{\longmapsto} \gamma$$
$$A \overset{g}{\rightarrow} B \overset{f}{\rightarrow} \Gamma$$ $$\alpha \overset{g}{\mapsto} \beta \overset{f}{\mapsto} \gamma$$
4.5. Lettres grecques
$ A B \Gamma $… $ \alpha \beta \gamma $…
4.6. Lettres cursives
\mathscr, minuscules et majuscules :
$$ \mathscr a \mathscr b \mathscr c \mathscr d \mathscr e \mathscr f \mathscr g \mathscr h \mathscr i \mathscr j \mathscr k \mathscr l \mathscr m \mathscr n \mathscr o \mathscr p \mathscr q \mathscr r \mathscr s \mathscr t \mathscr u \mathscr v \mathscr w \mathscr x \mathscr y \mathscr z $$
$$ \mathscr A \mathscr B \mathscr C \mathscr D \mathscr E \mathscr F \mathscr G \mathscr H \mathscr I \mathscr J \mathscr K \mathscr L \mathscr M \mathscr N \mathscr O \mathscr P \mathscr Q \mathscr R \mathscr S \mathscr T \mathscr U \mathscr V \mathscr W \mathscr X \mathscr Y \mathscr Z $$
\mathcal, uniquement pour les majuscules :
$$ \mathcal A \mathcal B \mathcal C \mathcal D \mathcal E \mathcal F \mathcal G \mathcal H \mathcal I \mathcal J \mathcal K \mathcal L \mathcal M \mathcal N \mathcal O \mathcal P \mathcal Q \mathcal R \mathcal S \mathcal T \mathcal U \mathcal V \mathcal W \mathcal X \mathcal Y \mathcal Z $$
4.7. Géométrie
$\mathscr D \perp \mathscr D'$
$\mathscr D_1~//~\mathscr D_2$
$\mathscr D_1 // \mathscr D_2$
$\mathscr D_1~/\!/~\mathscr D_2$
$\mathscr D_1 \parallel \mathscr D_2$
$\widehat{ABC}$
4.8. Fonctions de référence
$$\ln 3$$
$$\cos^2 \theta + \sin^2 \theta$$
4.9. Ensembles et probas
$$ P \left( \overline A \right) = 1 - P(A) $$
$$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$
$$ P(A \cap B) = P(A) × P_A(B) = P(B) × P_B(A) $$
$$P(X=k) = {n \choose k} p^k(1-p)^{n-k}$$
$$P(x \in A) = 1 - P(x \notin A)$$
4.10. Mise en forme dans les formules
$$ (((0×3 + \mathbf{2})×3 + \mathbf{0})×3 + \mathbf{1})×3 + \mathbf{2} $$
4.11. Parenthèses, crochets, accolades
$4! = 4 × \underbrace{3×2×1}_{3!}$
$S = \left\{ 2 \right\}$
4.12. Au-dessus et en-dessous
Espérance :
$$ E(F) \overset{(1)}{=} E(\frac{1}{n} X) \overset{(2)}{=} \frac{1}{n}E(X) $$
- définition de F
- propriété de l’espérance des lois de probabilité discrètes
Fractions continues :
$$\underset{j=1}{\overset{\infty}{\LARGE\mathrm K}}\frac{a_j}{b_j} =\cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\ddots}}}$$
4.13. Systèmes
$$ \left \{ \begin{array}{l} n = q × d + r \\\\ 0 \le r < d \end{array} \right. $$
$$\left \{ \begin{aligned} u_0 &= 1 \\\\ u_{n+1} &= 1 + \frac{4}{u_n}, \text{pour } n \in \mathbb N \\\\ \end{aligned} \right .$$
4.14. Poursuite d’égalités
$$\begin{aligned} 17 &= 5×3 + 2 &(1) \\\\ &= (1×3 + 2)×3 + 2 &(2) \\\\ &= 1×3^{2} + 2×3^1 + 2×3^0 &(3) \end{aligned}$$
- Division euclidienne de 17 par 3.
- Division euclidienne de 5 par 3.
- On développe les multiplications par 3, sachant que 31 vaut 3 et 30 vaut 1.
4.15. Limites
$\lim\limits_{n \to +\infty} u_n$
4.16. Intégrales
$\int_a^b f(x)~dx = F(b) - F(a) = \left[ F(x) \right]_a^b $$
4.17. Logique
$\neg$ $\lnot$ $\wedge$ $\vee$ $\Leftrightarrow$ $\Rightarrow$
$$\left( \overline{(P∧Q)} \right) \Leftrightarrow \left( \overline{P}∨\overline{Q} \right)$$ $$\left( \overline{(P \wedge Q)} \right) \Leftrightarrow \left( \overline{P} \vee \overline{Q} \right)$$
$$\left( P⇒Q \right) ⇔ \left( (¬P)∨Q \right)$$ $$\left( P \Rightarrow Q \right) \Leftrightarrow \left( (\neg P) \wedge Q \right)$$
4.18. Vecteurs
\vec vs \overrightarrow :
$$(O; \vec i; \vec j)$$ $$(O; \overrightarrow i; \overrightarrow j)$$
$$\vec{AB} = \vec {AC} + \vec {CB}$$ $$\overrightarrow{AB} = \overrightarrow {AC} + \overrightarrow {CB}$$
4.19. Matrices
$$ \begin{matrix} a & b \\\\ c & d \end{matrix} \begin{pmatrix} a & b \\\\ c & d \end{pmatrix} \begin{bmatrix} a & b \\\\ c & d \end{bmatrix} \begin{Bmatrix} a & b \\\\ c & d \end{Bmatrix} \begin{vmatrix} a & b \\\\ c & d \end{vmatrix} \begin{Vmatrix} a & b \\\\ c & d \end{Vmatrix} $$
$$\begin{pmatrix} 1 & a_1 & a_1^2 & \cdots & a_1^n \\\\ 1 & a_2 & a_2^2 & \cdots & a_2^n \\\\ \vdots & \vdots& \vdots & \ddots & \vdots \\\\ 1 & a_m & a_m^2 & \cdots & a_m^n \end{pmatrix}$$
$$\left[ \begin{array}{cc|c} 1&2&3\\ 4&5&6 \end{array} \right]$$
4.20. Diagrammes
4.20.1. Sans XyJax
$$ \require{AMSmath} \def\mapright#1{\xrightarrow{#1}} \def\mapdown#1{\Big\downarrow\rlap{\raise2pt{\scriptstyle{#1}}}} \begin{array}{ccc} A& \mapright{f} & B \\[3pt] \mapdown{g} & & \mapdown{g'} \\ A^*& \mapright{f^*} & B^* \end{array}\phantom{h} $$
$$ \require{AMSmath} \def\mapright#1{\xrightarrow{#1}} \def\mapdown#1{\Big\downarrow\rlap{\raise2pt{\scriptstyle{#1}}}} \def\mapup#1{\Big\uparrow\rlap{\raise2pt{\scriptstyle{#1}}}} \begin{array}{ccc} v_{n+1} & ? & v_n \\[3pt] \mapdown{\text{cste}} & & \mapup{\text{cste}} \\ u_{n+1}& \mapright{\text{précédent}} & u_n \end{array}\phantom{h} $$
4.20.2. Avec XyJax
XyJax est une extension pour Mathjax.
$$ \begin{xy} \xymatrix { U \ar@/_/[ddr]_y \ar@{.>}[dr]|{\langle x,y \rangle} \ar@/^/[drr]^x \\ & X \times_Z Y \ar[d]^q \ar[r]_p & X \ar[d]_f \\ & Y \ar[r]^g & Z } \end{xy} $$
4.21. Autres
Il y a au moins deux façons de définir une suite à partir d’une fonction réelle $f$ :
- Explicitement si $f$ est définie sur des entiers (au moins à partir
d’un certain entier), en écrivant : $$\forall n \ge n_0, u_n = f(n)$$
On dit aussi que la suite échantillonne la fonction $f$. - Par récurrence si $f$ est définie sur un sous-ensemble de $\mathbb R$ suffisamment bien choisi, en écrivant : $$\forall n \ge n_0, u_{n+1} = f(u_n)$$
5. Ditaa
Ditaa permet de convertir un schéma fait en texte plat (ou ascii art pour les connaisseurs) en image.
ASCII Flow peut grandement aider à la construction des diagrammes.
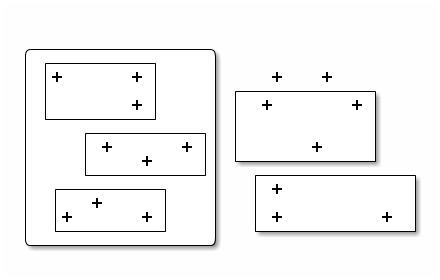
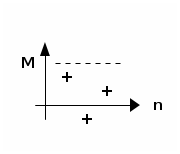
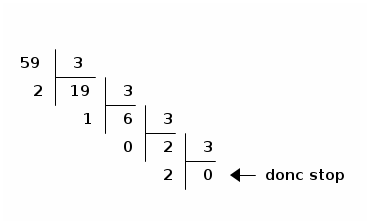
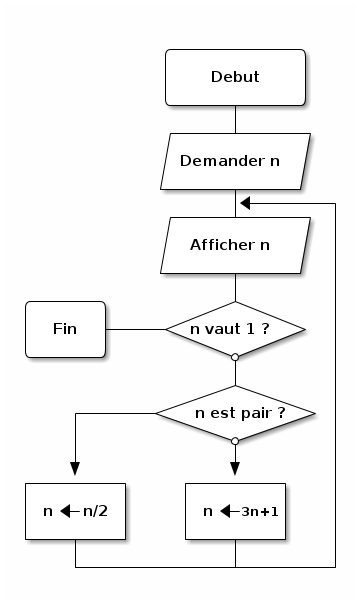
Attention, il n’est pas possible d’incorporer du texte avec des caractères autres qu’ascii.
6. JSXGraph
Les animations JSXGraph peuvent être incorporées grâce au fait que le HTML est laissé intact par Markdown.
En plus de l’exemple ci-dessous, vous pouvez allez admirer les meilleurs exemples, ou parcourir l’ensemble des exemples sur le site officiel.
Cliquez sur le bouton plot:
7. highlight.js
highlight.js s’occupe de la coloration syntaxique des fragments de code proposés au sein des pages.
Il colore automatiquement les portions de code source comprises entre les
balises <pre><code> et </code></pre>, du côté du client
(c’est à dire dans le navigateur). Plus les fragments sont petits, plus le
procédé est fragile. C’est pour cela que le langage reconnu est affiché en
bas à droite des blocs en violet très très subtil, pour contrôler.
Sinon, il est possible de forcer le langage en utilisant :
<pre><code class="le_langage">Première ligne
Deuxième ligne
...
Dernière ligne</code></pre>
7.1. Python
def fact(n):
return n and n*fact(n-1) or 1
7.2. Lisp
(de ack (X Y)
(cond
((=0 X) (inc Y))
((=0 Y) (ack (dec X) 1))
(T (ack (dec X) (ack X (dec Y)))) ) )
Vous aurez reconnu la fonction d’Ackermann-Péter ici écrite en Picolisp.
7.3. Haskell
quicksort :: Ord a => [a] -> [a]
quicksort [] = []
quicksort (p:xs) = (quicksort lesser) ++ [p] ++ (quicksort greater)
where
lesser = filter (< p) xs
greater = filter (>= p) xs
7.4. HTML
<!DOCTYPE html>
<html>
<head>
<title>Titre de la page</title>
<meta http-equiv="Content-Type" content="text/html; charset=UTF-8" />
<link rel="stylesheet" type="text/css" href="style.css" />
<link rel="stylesheet" type="text/css" media="screen" href="screen.css">
<link rel="stylesheet" type="text/css" media="print" href="print.css">
</head>
<body>Le contenu de la page</body>
</html>
7.5. CSS
div.toc ul {
list-style-type: decimal;
}
a:link {color:#337;}
a:visited {color:#333;}
a:hover {color:#000;}
a:active {color:#000;}
7.6. Pseudo-code
Demander n
Tant que n ne vaut pas 1
| Afficher n
| Si n est pair, alors
| | n <- n/2
| Sinon
| | n <- 3*n + 1
| Fin du Si
7.7. Inclusion de fichiers
1 def fact(n):
2 print("on me demande fact de", n)
3 if n == 1:
4 print("point d'appui, retournons 1")
5 return 1
6 else:
7 fact_preced = fact(n-1)
8 resultat = n * fact_preced
9 print("je retourne", n, "fois", fact_preced)
10 print("soit", resultat)
11 return resultat
12
13 print(fact(4))
8. Contenu escamotable
8.1. HTML simple
J’ai utilisé le code publié ici pour pouvoir cacher du contenu que je ne veux pas dévoiler tout de suite.
Notez que le contenu escamotable ne passe pas au travers de Markdown, il faut utiliser des balises HTML pour toute mise en forme spéciale, et notez aussi que le contenu escamotable et son bouton sont cachés lors de l’impression.
8.2. Mathjax
En effet, $u_{n+1} - u_n = u_n \left( \frac{u_{n+1} }{u_n} - 1 \right)$.
8.3. Code mis en forme par highlight.js
>>> l = [1, 2, 3, 4]
>>> l[0] # contenu à la position 0
1
>>> l[1] # à la position 1
2
>>> l[-1] # à la dernière position (-2 -> avant dernière…)
4
>>> l[1:3] # sous-liste à partir de la position 1 jusqu’à avant la position 3
[2, 3] # (le « avant » est strict, ce qui est cohérent avec range)
>>> l[1:] # sous-liste à partir de la position 1
[2, 3, 4]
>>> l[:3] # sous-liste avant la position 3 (strictement)
[1, 2, 3]
>>> l[:-1] # sous-liste avant la dernière position (strictement)
[1, 2, 3]
>>> l[-2:] # sous-liste à partir de l’avant-dernière position
[3, 4]8.4. Videos
9. Diaporamas
Voir cette présentation.
10. Online Python Tutor
Online Python Tutor permet de suivre ligne par ligne l’exécution d’un programme (relativement simple) écrit en Python.
Voici un exemple :
11. Processing.js
Pour plus d’explications, voir la section correspondante dans le memento Processing.
11.1. Depuis un fichier sur le serveur
11.2. Avec le code source dans la page
11.3. Intégration avec Blockly
12. Timeline
En raison d’un problème de compatibilité avec pre3d, il n’est pas possible
d’afficher une frise sur une même page que l’application « cube de
couleur » ci-dessous. Pour voir une telle frise, aller sur la page du
blog.
13. Pre3d
Voici deux exemples de visualisations, à manipuler à la souris :
- glisser-déposer pour tourner la figure autour des axes $x$ et $y$ (axes de l’écran si la caméra n’a pas tourné)
- en appuyant en même temps sur
CTRL, on se déplace en $x$ et $y$ - en appuyant en même temps sur
SHIFT, on se déplace en $z$ - en appuyant en même temps sur
CTRLetSHIFT, on ajuste la distance focale
Pour plus d’explications, voir le memento Pre3d.
14. Delicious
Je stocke et trie mes liens favoris sur Delicious. Les liens publics de mon compte tournent autour des maths, de l’informatique et de la musique. Le site promet d’aider à « trouver, retrouver et montrer » du contenu.
Je ne me sers pas de la fonctionnalité de découverte (trouver), basée sur les liens que le reste de la communauté stocke. En revanche, je retrouve des liens intéressants grâce au système de tags (ou labels ou étiquettes), et je montre certains liens que je trouve intéressants dans certains contextes grâce à l’API de Delicious. Exemple :
Voici des exemples d’applications Android libres :
