Arithmétique
1. Activité introductive
Voir cette page.
2. Division euclidienne
La division euclidienne a déjà été vue au chapitre Systèmes de numération.
Elle est absolument indispensable pour la compréhension de ce chapitre. En fait c’est la seule division qui y soit acceptable (cours et exercices). En effet, on n’écrira pas $q = \frac{n}{d}$ ou $q = n÷d$ mais $n = q×d$ ou $n = q×d + r$.
3. Multiples et diviseurs
3.1. Définition
Si a et b sont des entiers relatifs, on dira indifféremment :
- a est un multiple de b,
- a est divisible par b,
- b est un diviseur de a,
- b divise a,
s’il existe un entier relatif k tel que : a=k×b.
3.2. Exemples
- 6 est un multiple de 3,
- 6 est divisible par 3,
- 3 est un diviseur de 6,
- 3 divise 6,
- en effet, comme 6=2×3, on prend k=2.
- 0 est un multiple de tous les nombres, il suffit de prendre k=0.
- 0 ne peut diviser que 0.
- Tout nombre entier n est divisible par 1 et par lui-même. Il suffit de prendre respectivement k=n et k=1.
3.3. Propriété
Si a est un entier et b est un entier non nul, on a :
a est un multiple de b si et seulement si le reste de la division euclidienne de a par b est nul.
3.4. Critères de divisibilité
En plus de bien connaître les tables de multiplication, il est utile de connaître les critères de divisibilité par 2, 3 et 9, 6, 4, 5, 8 et 10. Ils sont listés dans cet article sur Wikipedia.
Certains critères peuvent être très visuels sur l’écriture du nombre, ou même très visuel dans le procédé (voir par exemple ce critère de divisibilité par 7 qui utilise un graphe, et qui est équivalent à cet énoncé).
4. Nombres premiers
4.1. Définition
Un nombre premier est un nombre entier positif qui a exactement deux
diviseurs (1 et lui-même).
Un nombre non premier différent de 0 et de 1 est dit composé.
4.2. Exemples et remarques
- 0 et 1 ne sont pas premiers.
- Premiers nombres premiers : 2; 3; 5; 7; 11; 13, 17…
- Premiers nombres composés :
- 4 = 2×2, 2 est un diviseur strict de 4 et c’est le seul, de même pour 9 (entre autres),
- 6; 8; 10 ont deux diviseurs stricts,
- 12 = 2×6 ou 12 = 3×4, donc 12 a quatre diviseurs stricts.
- Les nombres premiers forment une source intarissable de thèmes de recherche en mathématiques et ont des applications fondamentales dans le domaine de la cryptographie, entre autres.
- Il y a une infinité de nombres premiers. Des sites les répertorient, parfois par catégories :
- Pour plus de détails, voir l’article Wikipedia sur les nombres premiers.
4.3. Crible d’Ératosthène
(En anglais sieve.)
4.3.1. Principe
On commence par se fixer une limite d’étude, ici 40.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
- 1 n’est pas premier, on le raye.
- 2 est premier. Aucun de ses multiples n’est premier, on les raye. (on note que 2 est le seul nombre premier pair).
- Le prochain non rayé est 3. Il est donc premier. Mais aucun de ses multiples n’est premier, donc on les raye.
- Le prochain est 5…
4.3.2. Remarques
On remarque que l’on peut commencer par le carré du nombre dont on barre les multiples car, par exemple pour 5, les nombres de la forme $k×5$ ont déjà été traités pour $k<5$.
Inversement, ce carré ne peut pas être barré avant car, comme c’est un carré de nombre premier, il n’a pas de diviseur strict avant sa racine carrée.
Mais quand doit-on s’arrêter pour ne garder que les premiers inférieurs à 40 ? C’est l’objet de la prochaine propriété.
4.4. Propriété
Si un nombre n est composé, alors il admet un diviseur strict d tel que $ d \le \sqrt{n} $.
Remarque : Cette propriété sert surtout à limiter la vérification de primalité d’un nombre. En effet, si un nombre n’a pas de diviseur strict inférieur ou égal à sa racine carrée, cela suffit pour dire qu’il est premier.
Démonstration : Soit n un nombre composé. On note $d_1$ et $d_2$ des diviseurs stricts de n (peut-être égaux), tels que $n = d_1 × d_2$ (on parlera de diviseurs associés).
On suppose par l’absurde que $d_1 > \sqrt{n}$ et $d_2 > \sqrt{n}$. On a la chaîne d’égalités et d’inégalités suivante :
$$ n = d_1 × d_2 > \sqrt{n} × \sqrt{n} = n $$
Ce qui est impossible.
Éclaircissements :
C’est un peu comme les vases communicants. Sur les deux diviseurs associés, s’ils sont différents, un est petit, un est grand.
Dans l’exemple du crible d’Ératosthène, 62=36 et 72=49. Donc rayer jusqu’aux multiples de 5 suffit puisque :
- Les multiples de 6 ont été rayés en tant que multiples de 2.
- Il n’y aura pas de multiple de 7 inférieur à 40 à rayer, car :
- s’ils sont de la forme $k×7$ avec $k < 7$, il ont déjà été traités,
- s’ils sont de la forme $k×7$ avec $k \ge 7$, ils ne sont pas inférieurs à 40.
Pour plus de détails, voir l’article sur Wikipedia.
Pour vous entraîner, donner les nombres premiers inférieurs à 120.

4.5. Autres cribles
4.6. Décomposition en facteurs premiers
4.6.1. Introduction
Une bonne activité d’introduction est par exemple de décoder des
factogrammes.
Voir cet article.
4.6.2. Théorème
On admet que tout nombre entier naturel se décompose de manière unique en produit de facteurs premiers.
Exemple : Décomposition de 360.
360 | 2
180 | 2
90 | 2
45 | 3
15 | 3
5 | 5
1 |
On écrira 360=2×2×2×3×3×5, voire même 360=23×32×5.
4.7. Approfondissement
Voici différents documents qui permettent de visualiser les facteurs premiers ou d’en apprendre plus sur les nombres premiers :
- une très belle animation qui exhibe cette décomposition sous forme de diagrammes. On note que les puissances de 2 sont représentées par des ensembles de Cantor et les puissances de 3 par des tapis de Sierpinski.
- la même chose en statique :
- décroissant (pdf),
- croissant (pdf),
- avec code couleur (pdf),
- la même chose, mais avec un code couleur pour reconnaître les grands nombres,
- la même chose, en monstrueux,
- une video d’une heure et quart sur les nombres premiers.
4.8. Nombre de diviseurs
4.8.1. Sur un exemple
Tout d’abord, méditons l’exemple précédent :
En plus de 1 et 360, on remarque d’autres diviseurs de 360.
$$\begin{array}{ccll} 2 & \text{car} & 360 = 2 × (2×2×3×3×5) &= 2 × (2^2×3^2×5) \\\\ 2^2 & \text{car} & 360 = (2×2) × (2×3×3×5) &= 2^2 × (2^1×3^2×5) \\\\ 2^3 & \text{car} & 360 = (2×2×2) × (3×3×5) &= 2^3 × (2^0×3^2×5) \\\\ 3 & \text{car} & 360 = 3 × (2×2×2×3×5) &= (2^0×3^1×5^0) × (2^2×3^1×5^1) \\\\ 2×3 & \text{car} & 362 = (2×3) × (2×2×3×5) &= (2^1×3^1×5^0) × (2^2×3^1×5^1) \\\\ \end{array}$$
et d’autres combinaisons de 2; 3 et 5…
En fait pour créer un diviseur de 360, il suffit de choisir la puissance de :
- 2 entre 0; 1; 2 et 3,
- 3 entre 0; 1 et 2,
- 5 entre 0 et 1.
On peut représenter ces choix dans un arbres à trois étages, qui aura 4×3×2 feuilles.
4.8.2. Cas général
Dans le cas général, si $n = p_1^{m_1} × p_2^{m_2} × … × p_q^{m_q}$, alors $n$ a $(m_1 + 1)(m_2 + 1)…(m_q + 1)$ diviseurs.
4.8.3. Signe des diviseurs
Attention, ici nous n’avons considéré que les diviseurs positifs d’un nombre. Si les diviseurs négatifs font partie du décompte, il faut doubler le nombre de diviseurs.
5. Plus Grand Diviseur Commun
5.1. Activité d’introduction
Voir cette page. Cette activité peut même se faire en début de chapitre.
5.2. Définition
Soit deux entiers $a$ et $b$. On note $D(a)$ et $D(b)$ les ensembles de diviseurs de $a$ et de $b$ respectivement.
Le plus grand élément commun à ces deux ensembles, c’est-à-dire le plus grand élément de leur intersection, est appelé le plus grand diviseur commun de $a$ et de $b$ (greatest common divisor en anglais), et est noté $PGCD(a,b)$ ou $GCD(a,b)$ voire $a \wedge b$.
5.3. Exemples
$$\begin{aligned}
D(6) &= \left\{1;2;3;6\right\} \\\\
D(15) &= \left\{1;3;5;15\right\}
\end{aligned}$$
d’où $PGCD(6;15)=3$.
$$\begin{aligned}
D(24) &= \left\{1;2;3;4;6;8;12;24\right\} \\\\
D(18) &= \left\{1;2;3;6;9;18\right\}
\end{aligned}$$
d’où $PGCD(24;18)=6$.
5.4. Premières propriétés
- Le PGCD est symétrique.
- Il est intéressant de réfléchir sur la valeur de :
- PGCD(1,n)
- PGCD(n,n)
- PGCD(n,mn)
- PGCD(0,n)
- PGCD(0,0)
5.5. PGCD et facteurs premiers
Après décomposition en facteurs premiers, on obtient le PGCD de a et de b en choisissant pour chaque facteur la plus petite puissance disponible entre celle de $a$ et celle de $b$.
Exemple :
On a : $360 = 2^3 × 3^2 × 5$ et $75 = 3 × 5^2$. Pour mieux comprendre, écrivons les facteurs premiers les uns en dessous des autres.
$$\begin{aligned} 360 &= 2^3 & 3^2 & 5^1 \\\\ 75 &= & 3^1 & 5^2 \\\\ PGCD(360, 75) &= 2^0 & 3^1 & 5^1 = 15 \end{aligned}$$
5.6. Algorithme d’Euclide
5.6.1. Propriété de remplacement
Soit deux nombres entiers $a$ et $b$ non nuls. On écrit la division de $a$ par $b$ ainsi :
$$\left \{ \begin{array}{l} a = q × b + r \\\\ 0 \le r < b \end{array} \right.$$
On admet que les diviseurs communs à $a$ et à $b$ sont aussi les diviseurs communs de $r$ et $b$. Donc on a $PGCD(a,b) = PGCD(r,b)$.
Autrement dit, dans un calcul de PGCD, on peut remplacer un nombre par le reste de la division de ce nombre par l’autre nombre.
Exemple :
On a vu que PGCD(24,18)=6. Vérifions que le PGCD se conserve en remplaçant 24 par le reste de la division de 24 par 18. Ce reste étant 6, on doit calculer PGCD(6,18), qui vaut 6 car 18 est un multiple de 6.
5.6.2. L’algorithme en lui-même
Il consiste à effectuer le remplacement par le reste de manière répétée jusqu’à ce que le reste soit nul.
Le PGCD est le dernier reste non nul car pour $n≠0$, on a $PGCD(0,n)=n$.
De plus cet algorithme termine car le reste d’une division euclidienne est strictement inférieur au diviseur. On ne peut que tomber sur 0 au bout d’un nombre fini d’itérations.
5.7. Nombres premiers entre eux
5.7.1. Définition
Deux nombres sont dits premiers entre eux si leur PGCD vaut 1.
5.7.2. Exemples
- C’est le cas par exemple pour 28 et 15.
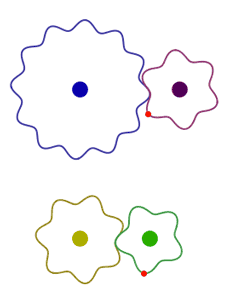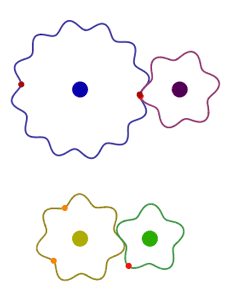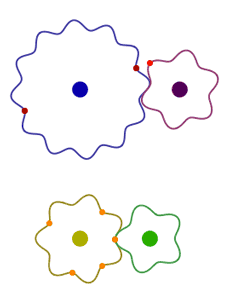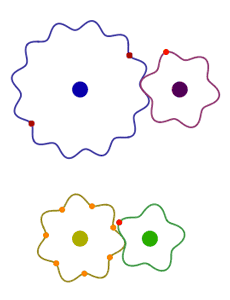
5.7.3. Méthodes
Pour savoir si deux nombres sont premiers entre eux, il suffit, au choix :
- d’utiliser l’algorithme d’Euclide,
- de les décomposer en facteurs premiers. En effet, deux nombres sont premiers entre eux si et seulement si ils n’ont aucun facteur premier en commun (voir cette propriété).
