Suites (1/2)
- Rappels
- Limites
- Convergence monotone
1. Rappels
Tempête cérébrale : qu’est-ce que le mot suite vous évoque ?
Pour la culture, voir l’OEIS.
1.1. Notations
Il y a plusieurs façons de nommer une suite, et l’on peut passer de l’une à l’autre assez librement.
Soit $u$ une suite et $u_n$ son terme d’indice (ou de rang) $n$.
- Si le premier terme de $u$ est $u_1$, alors $u$ est notée $(u_n)_{n \ge 1}$ ou $(u_n)_{n \in \mathbb N^*}$. Dans ce cas, $u_n$ est le $n$ème terme.
- Si le premier terme de $u$ est $u_0$, alors $u$ est notée $(u_n)_{n \ge 0}$ ou $(u_n)_{n \in \mathbb N}$. Dans ce cas, $u_n$ est le $n+1$ème terme !
- Attention, certaines suites peuvent commencer à un indice strictement supérieur à 1.
- Ne pas confondre $u_{n+1}$ et $u_n + 1$. $u_{n+1}$ est le terme qui suit $u_n$, qui a pour suivant $u_{n+2}$…
- On utilise parfois $v$ ou $w$… à la place de $u$.
Il y a, de plus, au moins deux façons de définir une suite à partir d’une fonction réelle $f$ :
- Explicitement si $f$ est définie sur des entiers (au moins à partir d’un certain entier), en écrivant : $$\forall n \ge n_0, u_n = f(n)$$ On dit aussi que la suite échantillonne la fonction $f$.
- Par récurrence si $f$ est définie sur un sous-ensemble de $\mathbb R$ suffisamment bien choisi, en écrivant : $$\forall n \ge n_0, u_{n+1} = f(u_n)$$ et en définissant un premier terme.
Schémas :
- points portés par la courbe ;
- axe avec une succession de flêches.
1.2. Majorants, minorants, bornes
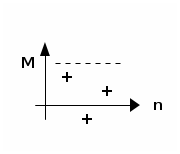
1.2.1. Définition : suite majorée
Une suite $u$ est majorée lorsque tous ses termes sont inférieurs à une même constante généralement notée $M$ appelée majorant.
Ainsi pour tout indice $n$, $u_n \le M$.
1.2.1.1. Remarques
- Les majorants ne sont pas uniques. Si $M$ est un majorant, tout nombre supérieur ou égal à $M$ en est aussi un.
- Une suite peut ne pas être majorée.
1.2.1.2. Exemples et contre-exemples
- Les suites constantes sont majorées.
- La suite $(u_n)=\left((-1)^n\right)$ est majorée par $M = 1$, mais aussi par tout nombre supérieur ou égal à 1.
- La suite $(u_n)=(sin(n))$ est majorée par $M = 1$, mais aussi par tout nombre supérieur ou égal à 1. En revanche, aucun nombre strictement inférieur à 1 ne majore $u$.
- La suite $(u_n)=(n)$ n’est pas majorée. Pour tout nombre réel $M$, aussi grand soit-il, il existe un terme de la suite qui lui est strictement supérieur.
1.2.2. Définition : suite minorée
Une suite $u$ est minorée lorsque tous ses termes sont supérieurs à une même constante généralement notée $m$ appelée minorant.
Ainsi pour tout indice $n$, $u_n \ge m$.
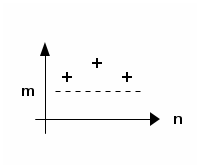
On peut facilement adapter les remarques et les exemples des suites majorées aux suites minorées.
1.2.3. Définition : suite bornée
Une suite est bornée si elle est à la fois minorée et majorée. Ainsi pour tout indice $n$, $m \le u_n \le M$.
1.2.3.1. Exemple et remarque
- La fonction inverse n’est pas bornée, mais la suite
$(u_n) = (\frac{1}{n})_{n \in \mathbb N^*}$ est bornée. En effet,
- comme la fonction inverse est décroissante, $n \ge 1$ entraîne $\frac{1}{n} \le 1$,
- comme $n$ est positif, $\frac{1}{n}\ \ge 0$.
- Pour être non bornée, une suite peut être soit non minorée, soit non majorée, soit ni l’un ni l’autre.
1.3. Variations
1.3.1. Définitions
- Une suite est croissante quand chaque terme est inférieur ou égal au suivant. Ainsi, pour tout indice $n$, $u_n \le u_{n+1}$.
- Une suite est décroissante quand chaque terme est supérieur au suivant. Ainsi, pour tout indice $n$, $u_n \ge u_{n+1}$.
1.3.1.1. Remarques
- C’est une définition par récurrence.
- Comme les suites sont assez souvent monotones (attention, pas toujours !), on demandera parfois d’ « étudier la monotonie de cette suite » plutôt que d’ « étudier les variations de cette suite ».
- Les variations d’une suite découlent du signe de $u_{n+1} - u_n$ (différence de termes consécutifs).
- Si les termes de la suite sont strictement positifs (c’est parfois difficile
à démontrer), il est aussi possible d’étudier le quotient
$\frac{u_{n+1}}{u_n}$ et de le comparer à 1.
En effet, $u_{n+1} - u_n = u_n \left( \frac{u_{n+1}}{u_n} - 1 \right)$. - La négation de croître n’est pas décroître.
- Une suite croissante est minorée par son premier terme, et une suite décroissante est majorée par son premier terme (sera démontré par récurrence plus tard).
1.3.1.2. Exemples
- Certaines suites sont ni croissantes ni décroissantes, comme par exemple $((-1)^n)$.
- Les suites constantes sont croissantes et décroissantes.
- Une suite arithmétique de raison $r$ est
- croissante si $r$ est positif,
- décroissante si $r$ est négatif.
- Une suite géométrique de premier terme positif et de raison q
est
- croissante si $q > 1$,
- décroissante si $0 < q < 1$.
1.4. Suites résultant de l’échantillonnage d’une fonction
1.4.1. Définition
On dit que la suite $u$ résulte de l’échantillonnage d’une fonction s’il existe une fonction $f$ de $\mathbb R$ dans $\mathbb R$ telle que pour tout indice $n$, $u_n = f(n)$.
On dit aussi que $f$ est la fonction dont la suite $u$ est extraite.
1.4.2. Propriétés
Si une fonction est croissante, décroissante, minorée, majorée ou bornée, toute suite résultant de son échantillonnage aura aussi cette propriété.
Attention, les réciproques sont fausses (trouver des contre-exemples).
1.4.2.1. ROC
Démontrer ces cinq dernières propriétés.
1.4.2.2. Exercice
Montrer de deux façons que $(-3n^2 + 5n + 2)_{n \in \mathbb N^*}$ est décroissante, une qui utilise la définition (version différence de termes consécutifs), une qui utilise l’étude d’une fonction.
2. Limites
2.1. Définitions
2.1.1. Limite infinie
2.1.1.1. Définition
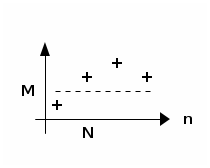
Une suite $u$ a pour limite $+\infty$ lorsque tout intervalle de la forme $\left[ M ; +\infty \right[$ contient tous les termes de la suite à partir d’un certain indice.
Autrement dit, pour tout nombre réel $M$ (destiné à être un grand nombre positif), il existe un rang $N$ (aussi destiné à être grand), à partir duquel les termes de la suite sont supérieurs à $M$.
Et avec plus de symboles mathématiques :
Pour tout $M \in \mathbb R$, il existe un indice $N$ tel que
$n \ge N \Rightarrow u_n \ge M$.
On notera $\lim\limits_{n \to +\infty} u_n = +\infty$, ou $\lim u = +\infty$.
Cette notation se lit : « la limite de $u_n$ quand $n$ tend vers l’infini vaut plus l’infini », ou simplement « la limite de $u$ est l’infini » voire même « $u_n$ tend vers l’infini quand $n$ tend vers l’infini ». « $u$ tend vers l’infini ».
2.1.1.2. Remarques
- L’intervalle $\left[ M ; +\infty \right[$ doit être en quelque sorte considéré comme « vertical », puisque c’est un intervalle de l’axe des ordonnées.
- $M$ est destiné à être un nombre arbitrairement grand.
- « à partir d’un certain indice » se dit parfois « sauf un nombre fini d’entre eux ».
- La définition d’une suite tendant vers $-\infty$ est semblable.
- Écrivez-la.
- On notera $\lim\limits_{n \to +\infty} u_n = -\infty$, ou $\lim u = -\infty$.
2.1.1.3. Exemples et contre-exemples
-
L'activité d'introduction nous a fourni trois suites qui tendent vers $+\infty$ : $(n)_{n \in \mathbb N}$, $(n^2)_{n \in \mathbb N}$ et $(\sqrt{n})_{n \in \mathbb N}$.
-
Les exemples précédents nous aident à trouver des suites tendant vers $-\infty$.
-
Attention, il existe des suites croissantes majorées (donc ne tendant pas vers $+\infty$), des suites non majorées mais qui ne tendent pas vers $+\infty$ et des suites non croissantes (à partir de n’importe quel rang), mais qui tendent quand même vers $+\infty$. Donner des exemples de telles suites.
2.1.2. Limite finie
2.1.2.1. Définition
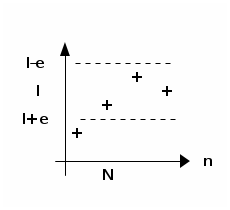
Une suite $u$ tend (ou converge) vers un nombre réel $l$ lorsque tout intervalle ouvert de la forme $\left] l - \epsilon; l + \epsilon \right[$ contient tous les termes de la suite à partir d’un certain indice.
$\epsilon$ est ici un nombre réel strictement positif, destiné à être petit.
Autrement dit, pour tout nombre réel $\epsilon$ strictement positif (destiné à être un petit nombre positif), il existe un rang $N$ (destiné à être grand), à partir duquel les termes $u_n$ de la suite sont tels que : $$u_n \in \left] l - \epsilon; l + \epsilon \right[$$ c’est-à-dire : $$l - \epsilon < u_n < l + \epsilon$$
On notera $\lim\limits_{n \to +\infty} u_n = l$, ou $\lim u = l$.
Cette notation se lit : « la limite de $u_n$ quand $n$ tend vers l’infini vaut $l$ », ou simplement « la limite de $u$ est $l$ » voire même « $u_n$ tend vers $l$ quand $n$ tend vers l’infini » ou plus simplement « $u$ tend vers $l$ ».
2.1.2.2. Remarques
- $\epsilon$ est destiné à être un nombre arbitrairement petit. Ainsi, les termes de la suite finissent par approcher $l$ à $\epsilon$ près.
- Parfois, on ne précise pas la limite et on dit simplement que « la suite converge » ou « est convergente ».
- Une suite qui ne converge pas diverge. Par exemple :
- $u_n = (-1)^n$, qui pourtant reste bornée,
- $u_n = n$, qui tend vers $+\infty$ (et qui possède pourtant une limite).
2.1.2.3. Exemples
L'activité d'introduction nous a fourni quelques exemples.
Exercice : Soit $(u)$ la suite définie pour $n$ entier naturel non nul par $u_n = \frac{1}{n}$. Montrer que cette suite tend vers 0.
2.1.2.4. Théorême
Une suite convergente est bornée.
Démonstration en exercice.
2.2. Exemples fondamentaux
2.2.1. Suites arithmétiques
Exercice : Suivant la raison $r$ d’une suite arithmétique, donner, si elle existe, sa limite.
Sinon, la suite tend vers $-\infty$ ou $+\infty$ suivant le signe de $r$.
Mais tout cela reste à démontrer…
2.2.2. Suites sans limite
Une suite peut ne pas avoir de limite. En voici quelques-unes qui montrent combien les situations peuvent être différentes :
| pour $n \in \mathbb N, u_n =$ | commentaire |
|---|---|
| $(-1)^n$ | bornée |
| $\cos (n \pi)$ | idem |
| $\cos (n)$ | bornée aussi, mais prend beaucoup de valeurs différentes |
| $n × \frac{\left( 1+(-1)^n \right)}{2}$ | minorée mais non bornée |
| $n×(-1)^n$ | ni minorée, ni majorée |
Dans ce cas, il ne faut pas utiliser la notation $\lim\limits_{n \to +\infty} u_n$, même quand on ne sait pas si la suite a une limite ou non. Cette notation est réservée aux suites qui ont une limite.
2.3. Théorême d’unicité de la limite
On admet que :
Lorsque qu’une suite converge, sa limite est unique.
2.4. Opérations sur les limites
Voir livre page 35.
Trouver des exemples de suites correspondants aux cas de formes indéterminées, en remplissant un tableau de la forme :
| Énoncé | Exemple 1 | Ex2 | … |
|---|---|---|---|
| $u_n$ | ? | ? | |
| $\lim u$ | $+\infty$ | $+\infty$ | |
| $v_n$ | ? | ? | |
| $\lim v$ | $-\infty$ | $-\infty$ | |
| $u_n + v_n$ | ? | ? | |
| $\lim (u+v)$ | 0 | $+\infty$ |
Il est possible d’obtenir pour limite de $u+v$ : $0$, $+\infty$, $-\infty$, $7$, voire même pas de limite du tout.
Puis même chose pour le produit et le quotient.
2.5. Comparaisons de suites et limites
Voir livre page 34.
2.6. Pour lever une forme indéterminée
Il existe une multitude de techniques pour lever une indéterminée. Voici quelques exemples.
2.6.1. Suite extraite de fonction polynôme
Considérons la suite définie par $u_n = n^2 -10n + 1$.
- Calculer ses premiers termes.
- Quelle semble être sa limite ?
- Calculer les termes $u_{10}$ et $u_{11}$ ?
- Doit-on changer d’avis concernant la limite ?
2.6.1.1. Définition
Les fonctions polynôme sont définies sur $\mathbb R$ par :
$$ \begin{aligned} f(x) &= \sum_{i = 0}^p a_i x^i \\\\ &= a_p x^p + a_{p-1} x^{p-1} + ... + a_2 x^2 + a_1 x + a_0 \\\\ &(a_p \ne 0) \end{aligned} $$
Ici $f$ est de degré $p$.
2.6.1.2. Exemples de polynômes
- On peut définir une fonction polynôme $f$ en posant par exemple $f(x) = 2 x^2 - 5 x - 1$. Celle-ci est de degré 2.
- Les fonctions affines et les fonctions constantes sont des polynômes. Leur degré respectif est 1 et 0 dans le cas général.
- Si $a \ne 0$, $a x^n$ est un monôme (polynôme à un terme) de degré $n$.
- $7 x^{25} - 1$ est un polynôme de degré 25.
- Le polynôme nul est la fonction constante dont la seule image est 0. Ce polynôme n’a pas vraiment de degré (ou par convention, on choisit $-\infty$).
2.6.1.3. Propriété
Si $u$ est définie pour tout indice $n$ par $u_n = f(n)$ où $f$ est une fonction polynôme, alors la limite de $u$ est celle du monôme de plus haut degré de $f$.
2.6.1.4. Exemple
On pose $u_n = 2 n^2 - 5 n + 1$. La suite $u$ a la même limite que celle de la suite $v$, où $v_n = 2 n^2$ (on a gardé le terme de plus haut degré). Comme $v$ tend clairement vers $+\infty$, $u$ aussi.
2.6.1.5. Démonstration
Soit $u$ la suite extraite d’une fonction polynôme. En prenant $a_p \ne 0$, on a :
$$ \begin{aligned} u_n &= a_p n^p + a_{p-1} n^{p-1} + a_{p-2} n^{p-2} + ... + a_2 n^2 + a_1 n + a_0 \\\\ &= a_p n^p \left( 1 + \frac{a_{p-1} n^{p-1}}{a_p n^p} + \frac{a_{p-2} n^{p-2}}{a_p n^p} + ... + \frac{a_2 n^2}{a_p n^p} + \frac{a_1 n}{a_p n^p} + \frac{a_0}{a_p n^p} \right) \\\\ &= a_p n^p \left( 1 + \frac{a_{p-1}}{a_p} \frac{1}{n} + \frac{a_{p-2}}{a_p} \frac{1}{n^2} + ... + \frac{a_2}{a_p} \frac{1}{n^{p-2}} + \frac{a_1}{a_p} \frac{1}{n^{p-1}} + \frac{a_0}{a_p} \frac{1}{n^p} \right) \\\\ \end{aligned} $$
Comme les termes de la forme $\frac{1}{n^?}$ tendent vers 0, la parenthèse tend globalement vers 1. En utilisant les propriétés de la limite d’un produit, on obtient que la suite $u$ a bien la même limite que $a_p n^p$.
Il peut être intéressant de mener les calculs de la démonstration sur un exemple, disons $u_n = 2 n^2 - 5 n + 1$.
À retenir :
Souvent, pour lever une indéterminée qui fait intervenir l’infini, on factorise par le terme qui semble « écraser » les autres.
2.6.2. Suite extraite de fonction rationnelle
2.6.2.1. Définition
Les fonctions rationnelles sont de la forme $R(x) = \frac{P(x)}{Q(x)}$, où $P$ et $Q$ sont des fonctions polynôme, $Q$ n’étant pas le polynôme nul.
2.6.2.2. Remarque étymologique
Un nombre rationnel peut être défini comme quotient d’entiers relatifs. Une fonction rationnelle peut être définie comme quotient de fonctions polynômes.
2.6.2.3. Exemples
- On peut définir une fonction rationnelle $f$ en posant par exemple $f(x) = \frac{3n^3 - 2n + 1}{5n^4 - 8n^2 - 1} $.
- En prenant $Q$ constant et non nul, $R$ est un polynôme (de même degré que $P$).
- Ne pas confondre la comparaison des valeur et la comparaison des vitesses de
croissance des valeurs. Par exemple, la suite de terme général
$\frac{n+1}{n}$ est une forme indéterminée de type $\frac{\infty}{\infty}$,
et même si $n+1>n$, ça ne veut pas dire que cette suite tend vers l’infini.
La forme qui permet de conclure est $1 + \frac{1}{n}$.
2.6.2.4. Propriété
Si $u$ est définie pour tout indice $n$ par $u_n = f(n)$ où $f$ est une fonction rationnelle, alors la limite de $u$ est celle du quotient des monômes de plus haut degré des numérateurs et dénominateurs de $f$.
2.6.2.5. Un exemple avant la démonstration
$$ \begin{aligned} u_n &= \frac{3n^3 - 2n + 1}{5n^4 - 8n^2 - 1} \\\\ &= \frac{3n^3 \left( 1 - \frac{2}{3n^2} + \frac{1}{3n^3} \right)} {5n^4 \left( 1 - \frac{8}{5n^2} - \frac{1}{5n^4} \right)} \\\\ &= \frac{3}{5} \frac{1}{n} \frac{\left( 1 - \frac{2}{3n^2} + \frac{1}{3n^3} \right)} {\left( 1 - \frac{8}{5n^2} - \frac{1}{5n^4} \right)} \\\\ \end{aligned} $$
2.6.2.6. Démonstration
Soit $f$ une fonction rationnelle et $u$ sa suite extraite. On a :
$$ \begin{aligned} u_n &= \frac{a_p n^p + a_{p-1} n^{p-1} + a_{p-2} n^{p-2} + ... + a_2 n^2 + a_1 n + a_0} {b_q n^q + b_{q-1} n^{q-1} + b_{q-2} n^{q-2} + ... + b_2 n^2 + b_1 n + b_0} \\\\ &= \frac{a_p n^p \left(1 + \frac{a_{p-1} n^{p-1}}{a_p n^p} + ... + \frac{a_0}{a_p n^p} \right)} {b_q n^q \left(1 + \frac{b_{q-1} n^{q-1}}{b_q n^q} + ... + \frac{b_0}{b_q n^q} \right)} \\\\ &= \frac{a_p n^p \left(1 + \frac{a_{p-1}}{a_p} \frac{1}{n} + ... + \frac{a_0}{a_p} \frac{1}{n^p} \right)} {b_q n^q \left(1 + \frac{b_{q-1}}{b_q} \frac{1}{n} + ... + \frac{b_0}{b_q} \frac{1}{n^q} \right)} \\\\ &= \frac{a_p}{b_q} \frac{n^p}{n^q} \frac{1 + \epsilon_1(n)}{1 + \epsilon_2(n)} \end{aligned} $$
où $\epsilon_1$ et $\epsilon_2$ sont des fonctions qui tendent vers 0 quand $n$ tend vers $+\infty$.
Comme $\frac{1 + \epsilon_1(n)}{1 + \epsilon_2(n)}$ tend vers 1, on a bien les trois cas suivants :
- si $p = q$, alors $\frac{n^p}{n^q} = 1$ et $u$ tend vers $\frac{a_p}{b_q}$,
- si $p < q$, alors $u$ tend vers 0,
- si $p > q$, $u$ tend vers $+\infty$ ou $-\infty$, suivant le signe de $\frac{a_p}{b_q}$.
2.6.3. Quantité conjuguée
En calculant, pour $a$ et $b$ positifs, $\left( \sqrt{a} + \sqrt{b} \right) \left( \sqrt{a} - \sqrt{b} \right)$, on obtient un moyen de lever une forme indéterminée de type $(+\infty) - (+\infty)$ lorsque l’on doit étudier une différence de racines carrées.
Il suffit de changer l’écriture problématique en multipliant par $\frac{\sqrt{a} + \sqrt{b}}{\sqrt{a} + \sqrt{b}}$.
Exemple : On pose pour $n$ entier naturel non nul : $u_n = \sqrt{n} - \sqrt{n-1}$. Quelle est la limite de la suite $u$ ?
2.6.4. Croissance comparée
Lors de l’étude des fonctions exponentielles et des fonctions logarithmes, nous obtiendrons des moyens de lever d’autres formes indéterminées.
3. Convergence monotone
On admet que :
- Toute suite réelle croissante et majorée converge.
- Toute suite réelle décroissante et minorée converge.
Attention, ce théorème nous dit qu’une suite décroissante et positive converge, mais ne nous donne pas sa limite. Tend-elle forcément vers 0 ?
