Fonction exponentielle
1. Définition et premières propriétés
1.1. Définition
1.1.1. Théorème
Il existe une unique fonction $f$, dérivable sur $\mathbb R$, telle que :
$$ \left \{ \begin{array}{l} f(0) = 1 \\\\ \text{pour tout}~ x \in \mathbb R \text{,}~ f'(x) = f(x) \end{array} \right. $$
Autrement dit :
$$ \left \{ \begin{array}{l} f(0) = 1 \\\\ f' = f \end{array} \right. $$
On note cette fonction $\exp$ (voir plus loin pour une autre notation) et on l'appelle la fonction exponentielle. Les parenthèses pourront être omise s’il n’y a pas ambiguïté. L’image de $x$ par cette fonction est donc notée :
- $\exp (x)$
- parfois $\exp x$
On a donc :
- $\exp(0) = 1$
- $\exp' = \exp$ soit pour tout $x$ réel $\exp'(x) = \exp(x)$.
Au passage, dans la démonstration, nous obtiendrons que cette fonction ne s'annule pas, et que pour tout $x \in \mathbb R$, $\exp(-x) = \frac{1}{\exp(x)}$.
1.1.2. Démonstration
L'existence sera démontrée dans un prochain chapitre.
Pour l'unicité, nous allons supposer qu'il existe deux fonctions $f$ et $g$ définies et dérivables sur $\mathbb R$ telles que :
$$ \begin{array}{ll} \left \{ \begin{array}{l} f(0) = 1 \\\\ f' = f \end{array} \right. & \left \{ \begin{array}{l} g(0) = 1 \\\\ g' = g \end{array} \right. \end{array} $$
Nous allons scinder le raisonnement en plusieurs étapes :
- montrer que $g$ ne s'annule pas en montrant que la fonction $p$ définie sur
$\mathbb R$ par $p(x) = g(x)×g(-x)$ est constante et vaut toujours 1,
- pour cela nous noterons $k$ la fonction définie sur $\mathbb R$ par $k(x) = g(-x)$,
- puis nous dériverons le produit,
- montrer que la fonction $q$ définie sur $\mathbb R$ par
$q(x) = \frac{f(x)}{g(x)}$ est constante et vaut toujours 1,
- pour cela nous dériverons le quotient.
Rappels :
Quelle est la dérivée d'un produit de fonctions ? d'un quotient de
fonctions ? d'une fonction composée à droite par une fonction
affine ?
Que dire d'une fonction dérivable dont la dérivée est nulle sur son ensemble
de définition ?
Première étape :
Pour tout $x \in \mathbb R$, on a :
$k'(x) = -g'(-x)$ (voir ci-dessus la dérivée de la composée à droite par une fonction affine avec $a = -1$ et $b = 0$)
$p'(x) = g'(x)×k(x) + g(x)×k'(x) = g'(x)×g(-x) + g(x)×(-g'(-x))$ (dérivée d’un produit et expression de $k'$ ci-dessus)
Or d'après les hypothèses, $g'=g$, d'où :
$p'(x) = g(x)×g(-x) + g(x)×(-g(-x)) = g(x)×g(-x) - g(x)×g(-x) = 0$.
$p$ est donc une fonction constante, qui vaut toujours une de ses valeurs, disons $p(0)$, c’est-à-dire :
$p(0) = g(0)g(-0) = g(0)g(0) = 1×1 = 1$.
Donc $g$ ne peut pas s'annuler car si jamais pour réel $x_0$ on avait $g(x_0) = 0$, on aurait :
$p(x_0) = g(x_0)×g(-x_0) = 0×g(-x_0) = 0 \ne 1$.
Au passage, nous obtenons que pour tout réel $x$, $g(-x) = \frac{1}{g(x)}$.
Seconde étape :
On montre de façon analogue que $q$ est constante et vaut 1.
Finalement, le numérateur et le dénominateur de $q$, c'est à dire $f$ et $g$, sont égaux sur $\mathbb R$.
1.2. Premières propriétés
1.2.1. Allure
1.2.1.1. À la calculatrice
Utiliser les touches 2nde et ln, puis X pour obtenir $e^X$ et tracer
la courbe représentative de la fonction exponentielle sur l’intervalle
$\left[3;-3\right]$.
Attention, pour la calculatrice, $e$ est considérée comme une fonction (attend un nombre), mais c’est en fait un nombre.
C’est la crosse de hockey.
1.2.1.2. Méthode d’Euler
Voir cette activité.
1.2.2. Propriétés déduites du théorème
La fonction exponentielle :
- prend pour valeur 1 en 0, et on note $e$ l'image de 1, avec
$e \approx 2,718$,
- Tu aideras à rappeler ta quantité à beaucoup de docteurs amis.
- Connaissant cinq décimales (2,71828) on peut facilement passer à neuf en ajoutant à nouveau les quatre dernières (2,71828 1828).
- est sa propre dérivée,
- ne s'annule pas,
- est strictement positive sur $\mathbb R$,
- est strictement croissante sur $\mathbb R$,
- est telle que l'image de l'opposé d'un réel est l'inverse de l'image de ce réel. Autrement dit : pour tout réel $x$, $exp(-x) = \frac{1}{exp(x)}$,
- est telle que l'image d'une somme est le produit des images. Autrement dit : pour tous réels $x$ et $y$, $\exp(x+y) = \exp(x) × \exp(y)$,
- est telle que l'image d'une différence est le quotient des images. Autrement dit : pour tous réels $x$ et $y$, $\exp(x-y) = \frac{\exp(x)}{\exp(y)}$,
- se comporte comme une puissance (voir les deux propriétés précédentes), et sera aussi notée $\exp(x) = e^x$.
Démonstrations :
- Donné par la définition. Pour la valeur approchée de $e$, voir cette
activité sur la méthode d’Euler.
La calculatrice donne une valeur approchée :
2ndeln (e^x)1= - Donné par la définition.
- Donné par la démonstration du théorème-définition.
- Par l'absurde. Supposons que l'exponentielle soit strictement négative en un réel $x_0$ (elle ne s'annule pas, donc inutile de considérer le cas où elle s'annule). Comme elle est continue sur $\mathbb R$ et comme on a à la fois $\exp(x_0) < 0$ et $\exp(0) = 1 > 0$, le théorème des valeurs intermédiaires nous donne un zéro de $\exp$, ce qui contredit la propriété précédente.
- Découle de la propriété précédente car $\exp$ est sa propre dérivée.
- Donné par la démonstration du théorème-définition.
- Sera démontré plus loin. C'est ce qu'on appelle la « relation fonctionnelle ».
- Utiliser la propriété sur la somme et celle sur l’opposé.
- On remarque que :
- $\exp(0) = 1 = e^0$ et $\exp(1) = e = e^1$,
- et pour tout $x$ entier naturel non nul :
$$\begin{aligned}
\exp(x) &= \exp (\underbrace{1+1+…+1}_{x}) &(1) \\\\
&= \underbrace{\exp(1)×\exp(1)×…×\exp(1)}_{x ~\text{fois}} &(2) \\\\
&= \underbrace{e×e×…×e}_{x ~\text{fois}} &(3) \\\\
&= e^x &(4)
\end{aligned}
$$
- $x$ est un entier, donc une somme de 1.
- Relation fonctionnelle, propriété précédente.
- $e$ est défini par $e = \exp(1)$.
- Notation puissance, étendue maintenant aux réels.
2. Propriétés analytiques de l'exponentielle
2.1. Limites
2.1.1. En plus l'infini
2.1.1.1. Propriété
$$\lim\limits_{x \to +\infty} \exp(x) = + \infty$$
2.1.1.2. Démonstration
Soit $g$ la fonction définie sur $\mathbb R$ par :
$$g(x) = \exp(x) -x$$
On a :
$$g'(x) = \exp(x) - 1 ~\text{et}~ g''(x) = \exp(x)$$
$g''$ est donc, comme l’exponentielle, strictement positive sur $\mathbb R$.
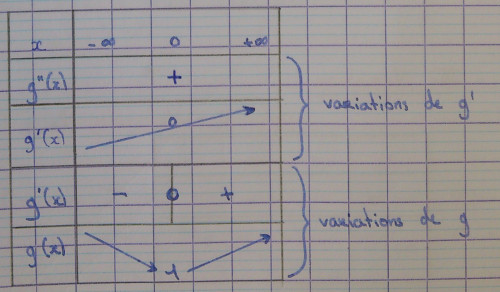
D'après le tableau de variations de $g$, on a pour tout réel $x$ :
$$\begin{aligned} g(x) & \ge 0 \\\\ \exp(x) - x & \ge 0 \\\\ \exp(x) & \ge x \end{aligned}$$
En appliquant le théorème de comparaison (dit « des sumos ») en $+\infty$, comme $\lim\limits_{x \to +\infty} x = + \infty$, on a bien $\lim\limits_{x \to +\infty} \exp(x) = + \infty$.
2.1.2. En moins l'infini
2.1.2.1. Propriété
$\lim\limits_{x \to -\infty} \exp(x) = 0$
2.1.2.2. Démonstration
$\lim\limits_{x \to +\infty} \exp(x) = + \infty$ d’où (en composant à gauche avec la fonction inverse, puis à droite par la fonction opposé) :
$ 0 = \lim\limits_{x \to + \infty} \frac{1}{exp(x)} = \lim\limits_{x \to + \infty} \exp(-x) = \lim\limits_{x \to - \infty} \exp(-(-x)) = \lim\limits_{x \to - \infty} \exp(x) $
On peut schématiser cette suite d’égalités ainsi :
x ---opp---> -x ---exp---> e^(-x) ---inv---> e^x
-oo +oo +oo O
2.2. Variations et représentation graphique
Exercice : On peut maintenant donner le tableau de variations complet, en complétant les premières propriétés par les limites.
Exercice : Tracer la courbe représentative de la fonction exponentielle dans un repère orthonormé. On pourra s'aider :
- d'un tableau de valeurs exactes et approchées,
- de trois droites importantes :
- une éventuelle asymptote,
- deux tangentes faciles à tracer, en 0 et en 1.
L'asymptote à la courbe est en $-\infty$ et est l'axe des abscisses.
Pour les tangentes, on peut au pire utiliser l'équation générale : $$y = f'(a)×(x-a) + f(a)$$ On note que la tangente en 1 passe par l'origine.
2.3. Compléments sur la dérivation
Ne jamais écrire $e'$, mais plutôt $\exp'$.
| Si $f(x)=…$ | alors $f'(x)=…$ |
|---|---|
| $e^{u(x)}$ | … |
| $e^{ax + b}$ | … |
| $e^{ax}$ | … |
| $e^{-x}$ | … (précédente avec $a=-1$ et $b=0$) |
| $e^{b}$ | … |
| $u(x)e^x$ | … |
| $u(x)e^{kx}$ | … |
| $\frac{e^x}{u(x)}$ | … |
| $\frac{u(x)}{e^x}$ | … (précédente avec $k=-1$) |
| $\frac{e^{kx} }{u(x)}$ | … |
| $\frac{u(x)}{e^{kx} }$ | … |
3. Propriétés algébriques de l'exponentielle
3.1. Fonction réciproque
On utilise ici un principe vu dans le chapitre précédent.
La fonction exponentielle étant continue sur $\mathbb R$, strictement croissante sur $\mathbb R$, et puisque $$\lim\limits_{- \infty} \exp = 0 ~\text{et}~ \lim\limits_{+ \infty} \exp = + \infty$$
On peut appliquer le théorème des valeurs intermédiaires (dans une de ses versions étendues). On obtient :
Pour tout $y \in \left]0; +\infty \right[$, il existe un unique réel $x$ tel que $$\exp(x) = y$$.
Ce $x$ est appelé le logarithme népérien de $y$ et est noté $x = \ln (y)$ ou, s'il n'y a pas ambiguïté $\ln y$. On définit ainsi sur $\mathbb R_+^*$ la fonction logarithme népérien. C'est la réciproque de la fonction exponentielle et elle sera étudiée plus en détail dans un autre chapitre.
En attendant, il faut savoir :
- que $\ln 1 = 0$,
- que $\ln e = 1$,
- comment utiliser sa calculatrice pour obtenir une valeur approchée du nombre dont l’exponentielle vaut 2.
3.2. Premières équations et inéquations
3.2.1. Équations avec deux exponentielles
3.2.1.1. Propriété
$$\exp(a) = \exp(b) ~\text{ssi}~ a = b$$
3.2.1.2. Démonstration
D'une part, si $a=b$, on a évidemment $\exp(a) = \exp(b)$.
D'autre part, comme $\exp$ est strictement monotone, deux réels différents ne peuvent avoir la même image.
3.2.1.3. Exemples
- Résoudre $\exp(x) = \exp(2)$.
- Résoudre $\exp(2x) = \exp(x+1)$.
- On a directement $x=2$ d'après la propriété, d’où $S = \left\{ 2 \right\}$.
- Cette équation est équivalente à $2x = x+1$, d’où $S = \left\{ 1 \right\}$.
3.2.2. Inéquations avec deux exponentielles
3.2.2.1. Propriétés
$$\exp(a) < \exp(b) ~\text{ssi}~ a < b$$
Ainsi qu'avec $>$, $\le$ et $\ge$.
3.2.2.2. Démonstration
Résultent du fait que $\exp$ est strictement croissante.
3.2.2.3. Exemples
- Résoudre $\exp(x) > \exp(2)$.
- Résoudre $\exp(2x) \le \exp(x + 1)$.
- On a directement $x>2$ d'après la propriété, soit $S = \left]2; +\infty\right[$.
- Cette équation est équivalente à $2x \le x+1$. $S = \left]-\infty ; 1 \right]$.
3.2.3. Utilisation de ln
Si l'un des deux membres est une constante, on peut se débarasser de l'exponentielle de l'autre membre en utilisant la fonction réciproque de l'exponentielle, la fonction logarithme népérien vue plus haut. En fait on peut ainsi retrouver toutes les propriétés précédentes, mais on a de plus, par exemple :
$$exp(x) = 2 ~\text{ssi}~ x = \ln 2 ~\text{d'où}~ S = \left\{\ln 2\right\}$$
$$exp(x) \le \frac{3}{2} ~\text{ssi}~ x \le \ln \frac{3}{2} ~\text{d'où}~ S = \left]-\infty; \frac{3}{2}\right]$$
Mais attention aux valeurs possibles de l'exponentielle (et donc au domaine de définition du logarithme) :
$$exp(x) = -2 ~\text{on a}~ S = \emptyset$$
$$exp(x) \ge -2 ~\text{on a}~ S = \mathbb R$$
3.2.4. Remarque
Les équations faisant apparaître à la fois $x$ et $e^x$, comme $e^x = x$ sont parfois très difficiles à résoudre de manière exacte, il faut savoir se contenter d’une méthode analytique plutôt qu'algébrique :
- l’existence d’une solution, est souvent donnée par le théorème des valeurs intermédiaires,
- une valeur approchée sera donnée par un logiciel ou par la calculatrice (avec sa fonction représentation graphique ou sa fonction tableau de valeurs).
3.3. Égalités et opérations
3.3.1. Relation fonctionnelle
Théorème :
Pour tous réels $x$ et $y$, on a $\exp(x+y) = \exp(x)×\exp(y)$.
Démonstration :
On fixe $y$ et on définit sur $\mathbb R$ la fonction $f$ par :
$$f(x) = \frac{\exp(x+y)}{\exp(x)}$$
$f$ est dérivable sur $\mathbb R$ en tant que quotient de fonctions dérivables, avec :
$$f'(x) = \frac{\exp(x+y)\exp(x) - \exp(x+y)\exp(x)}{(\exp(x))^2} = 0$$
$f$ est donc constante avec pour tout réel $x$ :
$$\frac{\exp(x+y)}{\exp(x)} = f(x) = f(0) = \frac{\exp(0+y)}{\exp(0)} = \frac{\exp(y)}{1} = \exp(y)$$
D'où le résultat en multipliant par $\exp(x)$, pour tous $x$ et $y$.
Remarques :
- Cette démonstration vaut aussi pour les fonctions de la forme $x \mapsto \exp(kx)$.
- La fonction $\exp$ est ainsi une sorte de suite géométrique continue :
En effet, d'une part pour tout réel $x$ :
$$\frac{\exp(x+1)}{\exp(x)} = \left(\frac{\text{terme suivant}}{\text{terme}}\right) = \frac{\exp(x)\exp(1)}{\exp(x)} = \exp(1) = e$$
et même :
$$\frac{\exp(x+\Delta)}{\exp(x)} = \exp(\Delta)$$
Et d'autre part elle s'écrit comme une puissance de $e$ (expression explicite d’une suite géométrique).
3.3.2. Autres égalités
Pour tout réel $x$ et pour tout entier naturel $n$ :
- $\exp(-x) = \frac{1}{\exp(x)}$
- $\exp(x-y) = \frac{\exp(x)}{\exp(y)}$
- $\exp(nx) = \left( \exp(x) \right)^n$
- $\exp(\frac{x}{n}) = \sqrt[n]{\exp(x)}$ et en particulier $\exp(\frac{x}{2}) = \sqrt{\exp(x)}$
Démonstrations :
1) C'est une des premières propriété que l'on ait démontrée, mais ce petit calcul est intéressant par lui-même :
$$\exp(x) \exp(-x) = \exp(x-x) = \exp(0) = 1$$
Puis on divise par $\exp(x)$ qui est non nul.
2) On combine la relation fonctionnelle et la propriété précédente en observant que $x - y = x + (-y)$.
3) Par récurrence (voir cette section du chapitre suivant).
4) Rappel : Pour $X>0$, $\sqrt[n]{X}$ est le nombre qui, mis à la puissance $n$, donne $X$. Par exemple, $\sqrt[3]{8} = 2$ car $2^3 = 8$.
Il suffit donc de calculer $\left[ \exp \left( \frac{x}{n} \right) \right]^n$ pour montrer cette propriété.
4. Autres limites
4.1. Croissance comparée
$$\lim\limits_{x \to + \infty} \frac{\exp(x)}{x} = + \infty$$
$$\lim\limits_{x \to + \infty} \frac{x}{\exp(x)} = 0^+$$
$$\lim\limits_{x \to + \infty} x \exp(-x) = 0^+$$
$$\lim\limits_{x \to - \infty} x \exp(x) = 0^-$$
Démonstrations :
Pour la première, voir l'exercice n°61 p.183.
Les autres découlent de la première en composant adéquatement par les
fonctions inverse ou opposé.
Remarque : Nous démontrerons dans un prochain chapitre que l’exponentielle croît plus vite que n’importe quelle puissance.
4.2. Approximation affine en 0
4.2.1. Propriétés
- $\lim\limits_{x \to 0} \frac{exp(x) - 1}{x} = 1$
- Il existe une fonction $\epsilon$ définie et continue sur $\mathbb R$ telle
que :
- $\lim\limits_{x \to 0} \epsilon(x) = 0$
- $\exp(x) = 1 + x + x \epsilon(x)$
On écrit parfois $\exp(x) \approx 1+x$ lorsque $x$ tend vers 0. C'est lié à la tangente en 0 que l'on a étudiée au début de ce cours.
4.2.2. Démonstrations
1) Comme $\exp$ est dérivable en 0, on a :
$$\lim\limits_{h \to 0} \frac{\exp(0+h) - \exp(0)}{h} = \exp'(0) = \exp(0) = 1$$
D'où le résultat en changeant de notation : $x$ à la place de $h$.
2) Il suffit de poser :
$$ \begin{aligned} \epsilon(x) &= \frac{exp(x) - 1}{x} - 1 & ~\text{pour}~ x \ne 0 \\\\ \epsilon(0) &= 0 & \end{aligned} $$
4.2.3. Exemples d'utilisation
$$ \begin{array}{c|ccccc} h & 0 & 0,001 & 0,01 & 0,1 & 0,5 \\\\ \hline e^h & 1 & & \approx 1,01005 & \approx 1,105 & \approx 1,65 \\\\ 1+h & 1 & 1,001 & 1,01 & 1,1 & 1,5 \\\\ e^h - (1 + h) & 0 & & & & \\\\ \end{array} $$
Ce genre d’approximation est très utilisé en physique, par exemple pour le pendule simple (voir cette section de l’article Wikipedia), où l’on approche $\sin(\theta)$ par $\theta$.
5. Synthèse
5.1. En résumé
$\exp$ est définie, continue et dérivable sur $\mathbb R$.
$\exp ' = \exp$ (elle est sa propre dérivée)
$\exp(0) = 1$
$\exp$ est strictement positive et strictement croissante sur $\mathbb R$.
Pour tout $y>0$, il existe un unique réel $x$ tel que $\exp(x) = y$, noté $x = \ln y$.
Entre autres égalités, on a pour tous réels $x$ et $y$ :
$$\exp(x+y) = \exp(x)×\exp(y)$$
En notant $\exp(1) = e \approx 2,718$, on a pour tout réel $x$, $\exp(x) = e^x$.
5.2. Jeu avec les notations
Il est recommandé de réécrire toutes les formules de ce cours avec la notation puissance.
